
【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:![]() ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.

(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
【答案】(1)30(2)34.6米
【解析】试题分析:(1)根据俯角以及坡度的定义即可求解;
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
试题解析:(1)∵山坡的坡度i(即tan∠ABC)为1:![]() .
.
∴tan∠ABC=![]() ,∴∠ABC=30°;∵从P点望山脚B处的俯角60°,
,∴∠ABC=30°;∵从P点望山脚B处的俯角60°,
∴∠PBH=60°,∴∠ABP=180°﹣30°﹣60°=90°故答案为:90.
(2)由题意得:∠PBH=60°,∵∠ABC=30°,∴∠ABP=90°,∴△PAB为直角三角形,
又∵∠APB=45°,在直角△PHB中,PB=PH÷sin∠PBH=45÷![]() =30
=30![]() (m).
(m).
在直角△PBA中,AB=PBtan∠BPA=30![]() ≈52.0(m).
≈52.0(m).
故A、B两点间的距离约为52.0米.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
(1)求抛物线的函数关系式;
(2)求△MCB的面积;
(3)设点P是直线l上的一个动点,当PA+PC最小时,求最小值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滨州苏宁电器超市销售每台进价分别为190元、160元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1720元 |
第二周 | 4台 | 10台 | 2960 元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5100元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
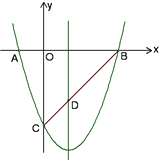
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ ![]() 时,求tan∠CED的值;
时,求tan∠CED的值;
②当以C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
(参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是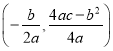 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列各式分解因式时应提取的公因式:
(1)ax-ay应提取的公因式是________;
(2)3mx-6nx2应提取的公因式是__________;
(3)-x2+xy-xz应提取的公因式是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐标平面上有一点A,且点A到x轴的距离为3,点A到y轴的距离恰为点A到x轴距离的2倍.若点A在第二象限,则点A的坐标为( )
A. (-3,6) B. (-3,2) C. (-6,3) D. (-2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为□ABCD的对角线,按要求完成下列各题.

(1)用直尺和圆规作出对角线BD的垂直平分线交AD于点E,交BC于点F,垂足为O.(保留作图痕迹,不要求写作法)
(2)在(1)的基础上,连接BE和DF.求证:四边形BFDE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com