
【题目】已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
(1)求抛物线的函数关系式;
(2)求△MCB的面积;
(3)设点P是直线l上的一个动点,当PA+PC最小时,求最小值。

【答案】(1)抛物线的函数关系式为y=-x2+2x+3;(2)3;(3)![]()
【解析】试题分析:(1)根据待定系数法求出抛物线解析式;
(2)先求出直线BC与对称轴的交点,即可得出MN,再用面积之和即可得出结论;
(3)先根据抛物线的对称性,判断出点P是直线BC与抛物线的对称轴l的交点,根据(2)直接得出点P坐标.
试题解析:(1)∵抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,
∴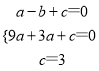 ,
,
∴ ,
,
∴抛物线的函数关系式为y=-x2+2x+3;
(2)如图1,

由(1)知,抛物线的函数关系式为y=-x2+2x+3;
∴抛物线的对称轴为x=1,M(1,4),
∵B(3,0)、C(0,3),
∴直线BC解析式为y=-x+3,
当x=1时,y=2,
∴N(1,2).
∴MN=2,OB=3,
∴S△MCB=S△MNC+S△MNB=![]() MN×OB=
MN×OB=![]() ×2×3=3;
×2×3=3;
(3)如图2,
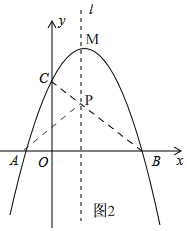
∵直线l是抛物线的对称轴,且A,B是抛物线与x轴的交点,
∴点A,B关于直线l对称,
∴PA+PC最小时,点P就是直线BC与直线l的交点,
由(2)知,抛物线与直线BC的交点坐标为(1,2),
∴点P(1,2).


科目:初中数学 来源: 题型:
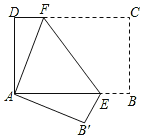
【题目】如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)证明:△ADF≌△AB′E;
(2)若AD=12,DC=18,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答
(1)探究:如图①,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,AE⊥CD于点E,若AE=8,求四边形ABCD的面积. 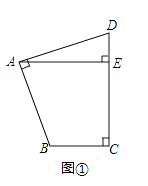
(2)应用:如图②,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,AE⊥BC于点E,若AE=20,BC=10,CD=6,则四边形ABCD的面积为 . 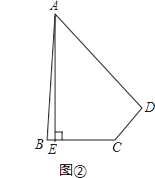
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“辽宁号”航母是中国海军航空母舰的首舰,标准排水量57000吨,满载排水量67500吨,数据67500用科学记数法表示为( )
A.675×102
B.67.5×102
C.6.75×104
D.6.75×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
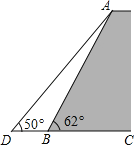
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:![]() ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.

(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A 1.5小时以上;B 1~1.5小时;C 0.5~1小时;D 0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题: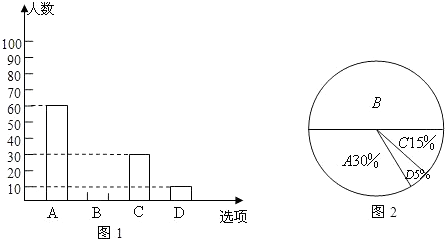
(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com