
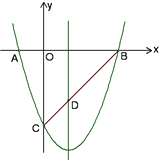
����Ŀ����ͼ��ʾ����֪������y��x2��bx��c��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C(0��-3)���Գ�����ֱ��x��1��ֱ��BC�������ߵĶԳ��ύ�ڵ�D��
��1���������ߵĺ�������ʽ��
��2����ֱ��BC�ĺ�������ʽ��
��3����EΪy����һ���㣬CE�Ĵ�ֱƽ���߽�CE�ڵ�F������������P��Q���㣬�ҵ�P�ڵ������ޣ�
�ٵ��߶�PQ ![]() ʱ����tan��CED��ֵ��
ʱ����tan��CED��ֵ��
�ڵ���C��D��EΪ�������������ֱ��������ʱ����ֱ��д����P�����꣮
���ο���ʽ��������![]() �Ķ���������
�Ķ���������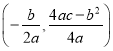 ��
��
���𰸡���1�������ߵĺ�������ʽΪ![]() ����2��ֱ��BC�ĺ�������ʽΪ
����2��ֱ��BC�ĺ�������ʽΪ![]() ����3����
����3����![]() ��
��![]() ��
�� 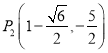 ��
��
�������������������1�����������ߵĶԳ��᷽�̿ɼ����b=-2���ٰ�C��0��-3�����������߽���ʽ�ɵõ�c=-3�����������ߵĺ�������ʽΪy=x2-2x-3��
��2��������������x��Ľ�������õ�A��-1��0����B��3��0����Ȼ�����ô���ϵ�������ֱ��BC�ĺ�������ʽ��
��3������AB=4��PQ=![]() AB=3�����������ߵĶԳ��Եõ�P���Q�����ֱ��x=1�Գƣ���P��-
AB=3�����������ߵĶԳ��Եõ�P���Q�����ֱ��x=1�Գƣ���P��-![]() ��-
��-![]() ��������F��0��-
��������F��0��-![]() ������FC=3-OF=
������FC=3-OF=![]() ������PQ��ֱƽ��CE�ڵ�F����CE=2FC=
������PQ��ֱƽ��CE�ڵ�F����CE=2FC=![]() ����D��1��-2��������D��DG��CE�ڵ�G����ͼ1����DG=1��CG=1������GE=CE=CG=
����D��1��-2��������D��DG��CE�ڵ�G����ͼ1����DG=1��CG=1������GE=CE=CG=![]() ��Ȼ����Rt��EGD�У��������еĶ�����⣻
��Ȼ����Rt��EGD�У��������еĶ�����⣻
����E��0��t�������������ľ��빫ʽ�õ�DE2=12+��t+2��2��CD2=12+��-2+3��2=2��EC2=��t+3��2��Ȼ��������ۣ�����CDE=90��ʱ��DE2+CD2=EC2����12+��t+2��2+2=��t+3��2������CED=90��ʱ��DE2+CE2=CD2����12+��t+2��2+��t+3��2=2������ECD=90��ʱ��CD2+CE2=DE2����2+��t+3��2=12+��t+2��2���ٷֱ�ⷽ�����tȷ��E�����꣬Ȼ����ݶ��κ���ͼ���ϵ����������ȷ��P�����꣮
���������
��1���������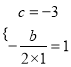 �� ���
�� ���![]() ��
��
���������ߵĺ�������ʽΪ![]() ��
��
��2����![]() =0����
=0����![]() ��
��
����A(-1��0)��B(3��0)��
��ֱ��BC�ĺ�������ʽΪ![]() ��
��
�����B(3��0)�͵�C(0��-3)����![]()
���![]() ��
��
����ֱ��BC�ĺ�������ʽΪ![]() ��
��
��3������ͼ2��ʾ����ΪAB��4������PQ![]() ����ΪP��Q����ֱ��x��1�Գƣ�
����ΪP��Q����ֱ��x��1�Գƣ�
���Ե�P�ĺ�����Ϊ![]() �� ���Ե�P������Ϊ
�� ���Ե�P������Ϊ![]() ����F������Ϊ
����F������Ϊ![]() ��
��
���� ![]() ��
�� ![]() ��
��
���� ![]() ����E������Ϊ
����E������Ϊ![]() ��
��
ֱ��BC: ![]() �������ߵĶԳ���x��1�Ľ���D������Ϊ��1����2����
�������ߵĶԳ���x��1�Ľ���D������Ϊ��1����2����
����D��DH��y�ᣬ����ΪH�� ��Rt��EDH�У�DH��1�� ![]() ��
��
����tan��CED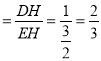 ��
��
����ͼ3��ͼ4�õ�P������Ϊ ![]() ��
�� 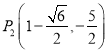 ��
��
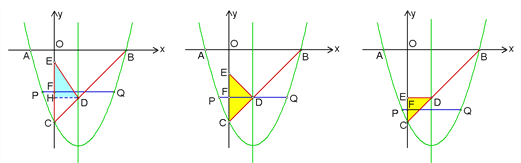
ͼ2 ͼ3 ͼ4
�㾦:�����Ƕ��κ������ۺ�����,�����漰����֪ʶ���������ߵĶ��㹫ʽ�������ε�������Լ��ô���ϵ������һ�κ����Ľ���ʽ�͵���ֱ�������ε�����,�����йض�������ʱҪע����������������۽��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCDΪ���Σ���PΪ�Խ���BD�ϵ�һ�����㣮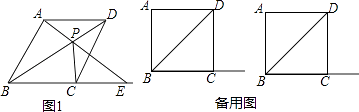
��1����ͼ1������AP���ӳ���BC���ӳ����ڵ�E������ PC����֤����AEB=��PCD��
��2����ͼ1����PA=PD��PC��BEʱ�����ABC�Ķ�����
��3������AP���ӳ�������BC�ڵ�E������ PC������ABC=90���ҡ�PCE�ǵ��������Σ����PEC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������
��1��̽������ͼ�٣����ı���ABCD�У���BAD=��BCD=90�㣬AB=AD��AE��CD�ڵ�E����AE=8�����ı���ABCD������� 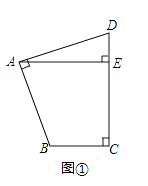
��2��Ӧ�ã���ͼ�ڣ����ı���ABCD�У���ABC+��ADC=180�㣬AB=AD��AE��BC�ڵ�E����AE=20��BC=10��CD=6�����ı���ABCD�����Ϊ �� 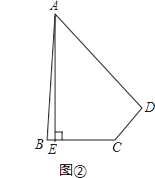
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
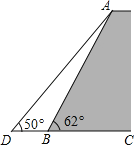
����Ŀ����ͼ��һ�̰ӵ��½ǡ�ABC=62�㣬���泤��AB=25�ף�ͼΪ����棩��Ϊ��ʹ�̰Ӹ����ι̣�һʩ�������ı�̰ӵ����棬ʹ��������½ǡ�ADB=50�㣬���ʱӦ���ӵ������ؿ������ף������������0.01�ף����ο����ݣ�sin62���0.88��cos62���0.47��tan50���1.20��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b�뷴�������� ![]() ��ͼ���ཻ��A��2��3����B����3��n�����㣮
��ͼ���ཻ��A��2��3����B����3��n�����㣮 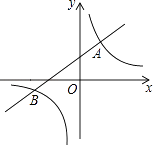
��1����һ�κ����뷴���������Ľ���ʽ��
��2������������������ֱ��д������ʽkx+b�� ![]() �Ľ⼯��
�Ľ⼯��
��3������OA��OB����S��ABO ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��С���ڴ�¥30�ߣ���PH��30�ף��Ĵ���P�����й۲⣬���ɽ����A���ĸ���Ϊ15�㣬ɽ��B���ĸ���Ϊ60�㣬��֪��ɽ�µ��¶�i����tan��ABC��Ϊ1��![]() ����P��H��B��C��A��ͬһ��ƽ���ϣ���H��B��C��ͬһ��ֱ���ϣ���PH��HC��
����P��H��B��C��A��ͬһ��ƽ���ϣ���H��B��C��ͬһ��ֱ���ϣ���PH��HC��

��1��ɽ���½ǣ�����ABC���Ķ������� �ȣ�
��2����ɽ��A��B�����ľ��루�����ȷ��0.1�ף���
���ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֵ
��1��5x2y+{xy��[5x2y����7xy2+ ![]() xy��]����4x2y+xy��}��7xy2 �� ����x=��
xy��]����4x2y+xy��}��7xy2 �� ����x=�� ![]() ��y=��16��
��y=��16��
��2��A=4x2��2xy+4y2 �� B=3x2��6xy+3y2 �� ��|x|=3��y2=16��|x+y|=1����4A+[��2A��B����3��A+B��]��ֵ��
��3�����m��3n+4=0����m��3n��2+7m3��3��2m3n��m2n��1��+3��m3+2m3n��m2n+n����m��10m3��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����Ϊ�ڶ���ʽ2x2+3x+1��һ������ʽ(x+1)������������ģ�2x2+3x+1=2x2+2x+x+1=2x(x+1)+(x+1)=(x+1)(2x+1).����Ϊ���������е������������Ϊ�е��������ſ���x2+3x+2����û����ʽ(x+1)���������Ϊû�е�������˵�����еĴ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ�����m��2��x��4mx��1��0��һԪ���η��̣���m��ȡ��Χֵ��_______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com