
【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.

【答案】(1)证明见解析(2)若AB⊥AD,则AEOF为正方形
【解析】试题分析:(1)利用SAS证明△ BCE≌△DCF;
(2)先证明AEOF为菱形,当BC⊥AB,得∠BAD=90°,再利用知识点:有一个角是90°的菱形是正方形。
试题解析:(1)∵四边形ABCD为菱形
∴AB=BC=CD=DA,∠B=∠D
又E、F分别是AB、AD中点,∴BE=DF
∴△ABE≌△CDF(SAS)
(2)若AB⊥AD,则AEOF为正方形,理由如下
∵E、O分别是AB、AC中点,∴EO∥BC,
又BC∥AD,∴OE∥AD,即:OE∥AF
同理可证OF∥AE,所以四边形AEOF为平行四边形
由(1)可得AE=AF
所以平行四边AEOF为菱形
因为BC⊥AB,所以∠BAD=90°,所以菱形AEOF为正方形。


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( ).

A.![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点D为BC的中点,点E与点C关于直线AD对称,CE与AD、AB分别交于点F、G,连接BE、BF、GD
求证:(1) △BEF为等腰直角三角形 ;(2) ∠ADC=∠BDG.

查看答案和解析>>
科目:初中数学 来源: 题型:
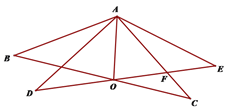
【题目】如图,△ABC和△ADE中,AB=AD,AC=AE, ∠BAC=∠DAE,BC交
DE于点O,∠BAD=a.
(1)求证:∠BOD=a.
(2)若AO平分∠DAC, 求证:AC=AD.
(3)若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组13名学生的一次英语听力测试成绩分布如下表所示(满分20分):
成绩(分) | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
人数(人) | 1 | 3 | 2 | 2 | 1 | 2 | 2 |
这13名学生听力测试成绩的中位数是( )
A.16分
B.17分
C.18分
D.19分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至北京时间2020年5月16日3时,全球新冠肺炎确诊病例超过4150000例,目前疫情依然持续蔓延.其中4150000用科学记数法表示应为( )
A.0.415×107B.4.15×106C.4.15×105D.415×104
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com