
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书.学校组织学生会成随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类.根据调查结果绘制了统计图(未完成).请根据图中信息,解答下列问题:

(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该学校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b﹣x的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )
A.k>1,b<0
B.k>1,b>0
C.k>0,b>0
D.k>0,b<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
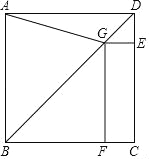
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程![]() ,操作步骤是:
,操作步骤是:
第一步:根据方程的系数特征,确定一对固定点![]() ;
;
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点![]() ,另一条直角边恒过点
,另一条直角边恒过点![]() ;
;
第三步:在移动过程中,当三角板的直角顶点落在![]() 轴上点
轴上点![]() 处时,点
处时,点![]() 的横坐标
的横坐标![]() 即为该方程的一个实数根(如图1);
即为该方程的一个实数根(如图1);
第四步:调整三角板直角顶点的位置,当它落在![]() 轴上另—点
轴上另—点![]() 处时,点
处时,点![]() 的横坐标
的横坐标![]() 即为该方程的另一个实数根.
即为该方程的另一个实数根.

(1)在图2中,按照“第四步”的操作方法作出点![]() (请保留作出点
(请保留作出点![]() 时直角三角板两条直角边的痕迹);
时直角三角板两条直角边的痕迹);
(2)结合图1,请证明“第三步”操作得到的![]() 就是方程
就是方程![]() 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程![]()
![]() 的实数根,请你直接写出一对固定点的坐标;
的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当![]() 与
与![]() 之间满足怎样的关系时,点
之间满足怎样的关系时,点![]() 就是符合要求的—对固定点?
就是符合要求的—对固定点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,△ABC的面积为40,则△DEF的面积为( )
A.60B.70C.80D.90
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com