Question

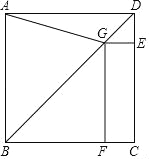
【题目】如图，在正方形ABCD中，点G在对角线BD上（不与点B，D重合），GE⊥DC于点E，GF⊥BC于点F，连结AG．

（1）写出线段AG，GE，GF长度之间的数量关系，并说明理由；

（2）若正方形ABCD的边长为1，∠AGF=105°，求线段BG的长．

Answer 1

【答案】（1）AG2=GE2+GF2（2）

【解析】

试题分析：（1）结论：AG2=GE2+GF2．只要证明GA=GC，四边形EGFC是矩形，推出GE=CF，在Rt△GFC中，利用勾股定理即可证明；

（2）作BN⊥AG于N，在BN上截取一点M，使得AM=BM．设AN=x．易证AM=BM=2x，MN=x，在Rt△ABN中，根据AB2=AN2+BN2，可得1=x2+（2x+x）2，解得x=，推出BN=，再根据BG=BN÷cos30°即可解决问题.

试题解析：（1）结论：AG2=GE2+GF2．

理由：连接CG．

∵四边形ABCD是正方形，

∴A、C关于对角线BD对称，

∵点G在BD上，

∴GA=GC，

∵GE⊥DC于点E，GF⊥BC于点F，

∴∠GEC=∠ECF=∠CFG=90°，

∴四边形EGFC是矩形，

∴CF=GE，

在Rt△GFC中，∵CG2=GF2+CF2，

∴AG2=GF2+GE2．

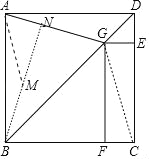
（2）作BN⊥AG于N，在BN上截取一点M，使得AM=BM．设AN=x．

∵∠AGF=105°，∠FBG=∠FGB=∠ABG=45°，

∴∠AGB=60°，∠GBN=30°，∠ABM=∠MAB=15°，

∴∠AMN=30°，

∴AM=BM=2x，MN=x，

在Rt△ABN中，∵AB2=AN2+BN2，

∴1=x2+（2x+x）2，

解得x=，

∴BN=，

∴BG=BN÷cos30°=．