
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①按对称轴公式x=-$\frac{b}{2a}$代入计算;
②利用配方法求顶点坐标,也可以利用顶点坐标公式(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)代入计算;
③求与y轴的交点?将x=0代入,求与x轴交点?将y=0代入,解二元一次方程;
④当a<0时,x>-$\frac{b}{2a}$时,y随x的增大而减小;x<-$\frac{b}{2a}$时,y随x的增大而增大.
解答 解:①对称轴=-$\frac{b}{2a}$=-$\frac{2}{2×(-1)}$=1,所以①正确;
②y=-x2+2x+3=-(x2-2x+1-1)+3=-(x-1)2+4,
∴它的顶点坐标为(1,4),所以②正确;
③y=-x2+2x+3,
当x=0时,y=3,
当y=0时,-x2+2x+3=0,x2-2x-3=0,
(x+1)(x-3)=0,
x1=-1,x2=3,
∴y=-x2+2x+3与y轴的交点为(0,3),与x轴的交点坐标为(-1,0)和(3,0),所以③正确;
④∵a=-1<0,
∴当x>1时,y随x的增大而减小,
所以④错误;
故正确的选项有①②③三个;
故选C.
点评 本题考查了二次函数的性质,是常考题型;本题除了利用二次函数的性质依次求解外,还可以利用画图象,观察图象求解.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
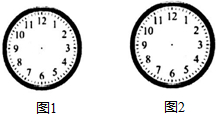 某电视台录制的“奔跑吧兄弟第四季”将在周五21:10播出,此时时钟上的分针与时针所成的角是多少度?在如图中大致标出此时的角(用短箭头、长箭头分别表示时针和分针),并用至少两种方式写出这个角?(可在表盘上标注相应的字母或数字)
某电视台录制的“奔跑吧兄弟第四季”将在周五21:10播出,此时时钟上的分针与时针所成的角是多少度?在如图中大致标出此时的角(用短箭头、长箭头分别表示时针和分针),并用至少两种方式写出这个角?(可在表盘上标注相应的字母或数字)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 栽后时间/年 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 树高/m | 2.0 | 2.6 | 3.2 | 3.8 | 4.4 | 4.8 | 5.2 | 5.6 | 6.0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
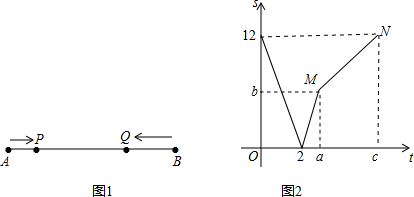
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y2>y3>y1 | C. | y2>y1>y3 | D. | y1>y3>y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com