

分析 (1)先用t表示出CN,AM,再通过线段和差关系表示出MB、BP;
(2)把t=3代入DN、BP中,若DN=BP,则四边形满足一组对边平行且相等,是平行四边形,否则就是梯形;
(3)①由于△BQM沿AB翻折成△MKB,只要QM=QB,四边形BQMK就是菱形,因为QP⊥AB,MP、BP可由t表示出来,可通过MP=PB计算出t;
②若四边形BQMK为正方形,则∠MQB是直角,∠QBA=45°,可通过等腰直角三角形间的三边关系,先求出t,再分别计算出BQ、DQ.
解答 解:(1)∵AB∥CD,AD⊥AB,AB=12,CD=9,过点N作NP⊥AB于点P,
∴四边形APND是矩形,
∴DN=AP.
∵AB=12,CD=9,AM=2t,CN=t,
∴DN=9-t,
∴BM=AB-AM=12-2t,BP=AB-AP=AB-DN=12-(9-t)=3+t.
答案:12-2t,3+t;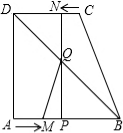
(2)当t=3时,DN=9-t=6,BP=3+t=6,
∴DN=PB,又∵DN∥BP,
∴四边形BNDP是平行四边形.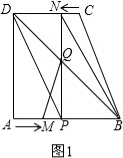
(3)①当t=1.5时,四边形BQMK为菱形.理由如下:
∵△BQM沿AB翻折,得△BKM,
∴BQ=BK,QM=MK,当QM=QB时,四边形MQBK是菱形.
∵QP⊥AB,
∴MP=BP.
∵MP=AP-AM=DN-AM=(9-t)-2t=9-3t,BP=AB-AP=AB-DN=3+t,
当9-3t=3+t时,t=1.5.即当t=1.5时,四边形BQMK为菱形.
②当菱形BQMK为正方形时,∠MQB=90°,BM=12-2t,BP=3+t,
∴∠QBM=45°.
∵cos∠MBQ=cos45°=$\frac{BQ}{BM}$=$\frac{BQ}{12-2t}$=$\frac{\sqrt{2}}{2}$,
∴BQ=6$\sqrt{2}$-$\sqrt{2}$t.
∵cos∠MBQ=cos45°=
$\frac{BP}{BQ}$=$\frac{3+t}{6\sqrt{2}-\sqrt{2}t}$=$\frac{\sqrt{2}}{2}$,即6+2t=12-2t,
解得t=1.5.∴BQ=6$\sqrt{2}$-1.5$\sqrt{2}$=4.5$\sqrt{2}$.
∵DC∥AB,
∴∠NDB=∠DBM=45°,
在RT△DNQ中,DQ=$\sqrt{2}$DN=(9-t)$\sqrt{2}$=7.5$\sqrt{2}$,
∴BD=BQ+DQ=4.5$\sqrt{2}$+7.5$\sqrt{2}$=12$\sqrt{2}$.
答案:12$\sqrt{2}$.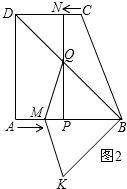
点评 点评:本题是一个直角梯形与动点的结合题目,考察了矩形的性质和判定、平行四边形的判定、菱形的性质及正方形的性质.等腰直角三角形的三边1:1:$\sqrt{2}$间关系或者特殊角的三角函数是解决本题的关键.


科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上,OC=3,OA=2$\sqrt{6}$,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为($\frac{6\sqrt{6}}{5}$,$\frac{3}{5}$).
如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上,OC=3,OA=2$\sqrt{6}$,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为($\frac{6\sqrt{6}}{5}$,$\frac{3}{5}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
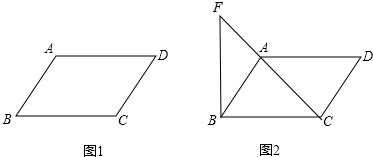
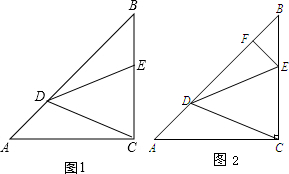 △ABC中,AC=BC,∠ACB=90°,点D,E分别在AB,BC上,且AD=BE,BD=AC.
△ABC中,AC=BC,∠ACB=90°,点D,E分别在AB,BC上,且AD=BE,BD=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com