

分析 (1)由x=2,可得AP=2,然后由y=S△APD=$\frac{1}{2}$AP•AD,求得答案;
(2)直接由y=S△APD=$\frac{1}{2}$AD•AB,求得答案;
(3)由已知得只有当点P在边AB或边CD上运动时,y=12,然后分别求解即可求得答案;
(4)首先作点A关于直线BC的对称点A1,连接A1D交BC于点P,则点P为所求;再证得△A1BP≌△DCP,即可求得答案.
解答 解:(1)如图2,∵AP=x=2,AD=6,∠A=90°,
∴y=S△APD=$\frac{1}{2}$AP•AD=6;
故答案为:6;
(2)如图3,y=S△APD=$\frac{1}{2}$AD•AB=$\frac{1}{2}$×6×6=18;
故答案为:18;
(3)解:由已知得只有当点P在边AB或边CD上运动时,y=12,
当点P在边AB上运动时,
∵S△PAD=$\frac{1}{2}$AD•PA,
∴$\frac{1}{2}$×6×PA=12,
解得PA=4,
即x=4;
当点P在边CD上运动时,
∵S△PAD=$\frac{1}{2}$AD×PD,
∴$\frac{1}{2}$×6×PD=12,
解得:PD=4,
∴x=AB+BC+CD=6+6+6-4=14;
综上所述,当y=12时,x=4或14;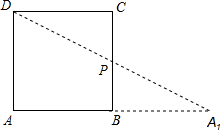 (4)解:作点A关于直线BC的对称点A1,连接A1D交BC于点P,则点P为所求.
(4)解:作点A关于直线BC的对称点A1,连接A1D交BC于点P,则点P为所求.
∴A1B=AB=CD=6,
∵∠PBA1=∠PBA=90°,∠C=90°,
∴∠PBA1=∠C,
在△A1BP和△DCP中,
$\left\{\begin{array}{l}{∠PB{A}_{1}=∠C}\\{∠BP{A}_{1}=∠CPD}\\{{A}_{1}B=CD}\end{array}\right.$,
∴△A1BP≌△DCP(AAS),
∴PB=PC=3,
∴x=AB+PB=9.
点评 此题属于四边形的综合题.考查了正方形的性质、全等三角形的判定与性质、最短路径问题以及动点问题.注意掌握分类讨论思想的应用是解此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
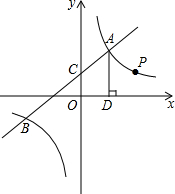 如图,一次函数y1=k1x+b 与反比例函数y2=$\frac{{k}_{2}}{x}$ 的图象交于点A(2,m)和B(-6,-2),与y轴交于点C.
如图,一次函数y1=k1x+b 与反比例函数y2=$\frac{{k}_{2}}{x}$ 的图象交于点A(2,m)和B(-6,-2),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
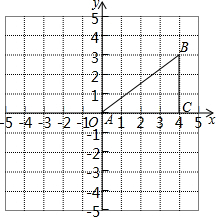 如图,坐标网格中的每个正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC的三个顶点A,B,C都在格点上,点A是坐标原点,AC在x轴的正半轴上.
如图,坐标网格中的每个正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC的三个顶点A,B,C都在格点上,点A是坐标原点,AC在x轴的正半轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x度时,应交电费为y元.具体收费情况如折线图所示,请根据图象回答下列问题:
某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x度时,应交电费为y元.具体收费情况如折线图所示,请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
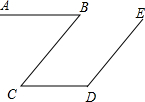 已知:如图所示,AB∥CD,∠B+∠D=180°.求证:BC∥DE
已知:如图所示,AB∥CD,∠B+∠D=180°.求证:BC∥DE查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com