
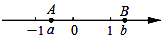 有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$+$\frac{|b-a|}{a-b}$-$\frac{1-b}{|1-b|}$的值是( )
有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$+$\frac{|b-a|}{a-b}$-$\frac{1-b}{|1-b|}$的值是( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 根据图示,可得-1<a<0,b>1,所以a+1>0,b-a>0,1-b<0,据此求出代数式$\frac{|a+1|}{a+1}$+$\frac{|b-a|}{a-b}$-$\frac{1-b}{|1-b|}$的值是多少即可.
解答 解:根据图示,可得-1<a<0,b>1,
∴a+1>0,b-a>0,1-b<0,
∴$\frac{|a+1|}{a+1}$+$\frac{|b-a|}{a-b}$-$\frac{1-b}{|1-b|}$
=$\frac{a+1}{a+1}$+$\frac{b-a}{a-b}$-$\frac{1-b}{b-1}$
=1-1+1
=1
故选:C.
点评 此题主要考查了数轴的特征和应用,以及绝对值的含义和应用,要熟练掌握,解答此题的关键是要明确:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com