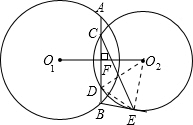
(1)证明:∵∠BED=30°,BE=DE,
∴∠BDE=∠EBD=75°.
∵BE是⊙O
2的切线,
∴∠BCE=∠BED=30°.
∴在△BCE中
∠CEB=180°-30°-75°=75°,
∴∠CEB=∠BEC.
∴BC=EC.
(2)解:∵AC、CE的长是方程x
2-10x+16=0的两个根且AC<CE,
∴x
1=2=AC,x
2=8=CE,
∵O
1O
2⊥AB于F,AB是⊙O
1的弦,
∴AF=BF;
∵CD是⊙O
2的弦,
∴CF=DF,
∴BD=AC=2;
∵BC=CE,
∴BC=CE=8,
∵BE是⊙O
2的切线,
∴BE
2=BD•BC=8×2=16,
∴BE=4,DE=4;
连接O
2E、O
2D,则BE⊥O
2E,
∵∠BED=30°,
∴∠DEO
2=60°,
∵O
2D=O
2E,
∴△DEO
2为正三角形,
∴O
2E=DE=4.
分析:(1)根据线切角等于它所夹弧所对的圆周角,得到∠BCE=∠BED,再根据BE=DE,∠BED=30°,得到∠CEB=75°,∠BEC=75°,即可得BC=EC;
(2)先由AC、CE的长是方程x
2-10x+16=0的两个根(AC<CE),求出AC、CE的长,再由O
1O
2⊥AB,根据垂径定理得到AF=BF,CE=DE,从而可得BD=AC,根据切割线定理求出DE的长,由于BE是圆的切线且∠BED=30°,判断出△DEO
2为正三角形,进而求出⊙O
2的半径.
点评:此题将两圆相交的条件以及和两圆相关的线段和角巧妙地结合起来,使之成为一个有机的整体,要充分利用它们之间的关系.

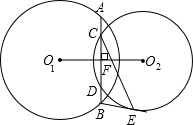 线BE,切点为E,连接EC、DE,若BE=DE,∠BED=30°,AC、CE的长是方程x2-10x+16=0的两个根(AC<CE).
线BE,切点为E,连接EC、DE,若BE=DE,∠BED=30°,AC、CE的长是方程x2-10x+16=0的两个根(AC<CE). (1)证明:∵∠BED=30°,BE=DE,
(1)证明:∵∠BED=30°,BE=DE,

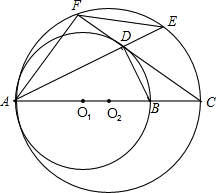 O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.
O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.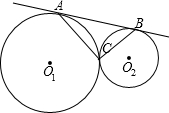 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=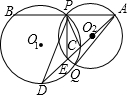 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且