Question

如果P是边长为4的等边三角形内任意一点，那么点P到三角形三边距离之和为    ．

Answer 1

【答案】分析：作出图形，根据等边三角形的性质求出高AH的长，再根据三角形的面积公式求出点P到三边的距离之和等于高线的长度，从而得解．
解答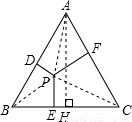：解：如图，∵等边三角形的边长为4，
∴高线AH=4×=2，
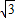
S_△ABC=BC•AH=AB•PD+BC•PE+AC•PF，
∴×4•AH=×4•PD+×4•PE+×4•PF，
∴PD+PE+PF=AH=2，
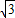
即点P到三角形三边距离之和为2．
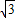
故答案为：2．
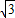
点评：本题考查了等边三角形的性质，根据三角形的面积求点P到三边的距离之和等于等边三角形的高是解题的关键，作出图形更形象直观．