
如果P是边长为4的等边三角形内任意一点,那么点P到三角形三边距离之和为
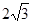
【解析】
试题分析:先根据题意画出图形,则有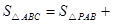
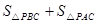 ,再根据三角形的面积公式可得h=PE+PF+PD,而等边三角形底边上的高等于边长乘以sin60°,即可求得结果.
,再根据三角形的面积公式可得h=PE+PF+PD,而等边三角形底边上的高等于边长乘以sin60°,即可求得结果.
如图所示,P是等边三角形ABC内一点,PD、PE、PF分别是点P到AB、BC、AB三边的垂线段,
连接PA、PB、PC,设此三角形BC边上的高是h,
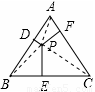
∵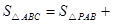
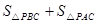
∴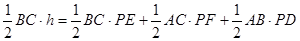
∵△ABC是等边三角形,
∴AB=BC=AC=2,
∴h=PE+PF+PD,
又∵等边三角形地边上的高h=边长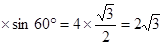
∴PE+PF+PD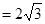 .
.
考点:等边三角形的性质,三角形的面积公式,特殊角的三角函数值
点评:解答本题的关键是能从图中看出三个小三角形的面积和等于大三角形的面积.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com