解答:
解:(1)如图①,连接PB,过点P作PM⊥x轴于点M.
由题意可知,OM=PM=m,PB=
m.
在Rt△PBM中,由勾股定理得:
BM=
=
=2m,
∴OB=OM+BM=m+2m=3m,
∴B(3m,0);
连接PD,过点P作PN⊥y轴于点N,同理可求得DN=2m,OD=3m.
过点D作DR⊥PE于点R,
∵平行四边形DOPE,∴∠ODE+∠DOP=180°;
由题意可知,∠DOP=45°,∴∠ODE=135°,
∴∠EDR=45°,即△EDR为等腰直角三角形,
∴ER=DR=OM=m,EM=ER+RM=ER+OD=m+3m=4m,
∴E(m,4m).
(2)相等.理由如下:

依题意画出图形,如图②所示.
由(1)知,∠ODE=∠BDO+∠BDE=135°,
又OB=OD=3m,即△OBD为等腰直角三角形,∴∠BDO=45°,
∴∠BDE=90°,即△BDE为直角三角形.
由圆周角定理可知,BE为△BDE外接圆的直径,∴∠BQE=90°.
过点E作EK⊥y轴于点K,则有EK=m,OK=4m.
∵∠BQE=90°,∴∠EQK+∠BQO=90°,又∠BQO+∠QBO=90°,
∴∠EQK=∠QBO.
∴Rt△EQK∽Rt△QBO,
∴
=,即
=,解得OQ=m或OQ=3m,
∵点Q与点D不重合,∴OQ=m,
∴OQ=EK,即相似比为1,此时两个三角形全等,
∴BQ=EQ.
(3)如图②所示,连接BC.
由(1)可知,如图①,CD=2DN=4m,∴OC=CD-OD=m.
由(2)可知,△BDE为直角三角形,△EDK与△BDO均为等腰直角三角形,
∴DE=
EK=
m,BD=
OB=3
m.
在Rt△BDE与Rt△BOC中,OC=m,OB=3m,DE=
m,BD=3
m,
∴
=,∴Rt△BDE∽Rt△BOC,
∴∠OBC=∠DBE,
∴∠DBC-∠DBE=(∠OBD+∠OBC)-∠DBE=∠OBD=45°.

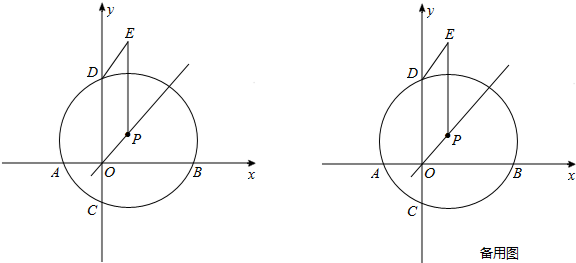
 解:(1)如图①,连接PB,过点P作PM⊥x轴于点M.
解:(1)如图①,连接PB,过点P作PM⊥x轴于点M.


 考前必练系列答案
考前必练系列答案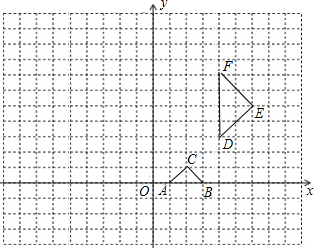 EF拼接成一个平行四边形(非正方形),写出符合要求的变换过程.
EF拼接成一个平行四边形(非正方形),写出符合要求的变换过程.