
如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.
(1)y=-x2+2x+3;(2)8;(3)点G不在该抛物线上.
解析试题分析:(1)在矩形OCEF中,已知OF、EF的长,先表示出C、E的坐标,然后利用待定系数法确定该函数的解析式.
(2)根据(1)的函数解析式求出A、B、D三点的坐标,以AB为底、D点纵坐标的绝对值为高,可求出△ABD的面积.
(3)首先根据旋转条件求出G点的坐标,然后将点G的坐标代入抛物线的解析式中直接进行判定即可.
(1)∵四边形OCEF为矩形,OF=2,EF=3,
∴点C的坐标为(0,3),点E的坐标为(2,3).
把x=0,y=3;x=2,y=3分别代入y=-x2+bx+c中,
得 ,
,
解得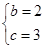 ,
,
∴抛物线所对应的函数解析式为y=-x2+2x+3;
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线的顶点坐标为D(1,4),
∴△ABD中AB边的高为4,
令y=0,得-x2+2x+3=0,
解得x1=-1,x2=3,
所以AB=3-(-1)=4,
∴△ABD的面积= ×4×4=8;
×4×4=8;
(3)△AOC绕点C逆时针旋转90°,CO落在CE所在的直线上,由(2)可知OA=1,
∴点A对应点G的坐标为(3,2),
当x=3时,y=-32+2×3+3=0≠2,所以点G不在该抛物线上.
考点:二次函数综合题.


科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(-2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.
(1)求抛物线的函数表达式;
(2)经过B,C的直线l平移后与抛物线交于点M,与x轴交于点N,当以B,C,M,N为顶点的四边形是平行四边形时,求出点M的坐标;
(3)若点D在x轴上,在抛物线上是否存在点P,使得△PBD≌△PBC?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间 (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数 (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当 =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示,已知两点A(-1,0),B(4,0),以AB为直径的半圆P交y轴于点C.
(1)求经过A、B、C三点的抛物线的解析式;
(2)设弦AC的垂直平分线交OC于D,连接AD并延长交半圆P于点E, 与
与 相等吗?请证明你的结论;
相等吗?请证明你的结论;
(3)设点M为x轴负半轴上一点,OM= AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线y=ax2+2x+c的顶点为A(―1,―4),与y轴交于点B,与x轴负半轴交于点C.
(1)求这条抛物线的函数关系式;
(2)点P为第三象限内抛物线上的一动点,连接BC、PC、PB,求△BCP面积的最大值,并求出此时点P的坐标;
(3)点E为抛物线上的一点,点F为x轴上的一点,若四边形ABEF为平行四边形,请直接写出所有符合条件的点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(11分)如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)点M是抛物线上的一个点,直线MN平行于y轴交直线AB于N,如果以M、N、B、C为顶点的四边形是平行四边形,求出点M的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 经过A(
经过A( ,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.
,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.
(1)求此抛物线的解析式及顶点坐标;
(2)若将此抛物线平移,使其顶点为点D,需如何平移?写出平移后抛物线的解析式;
(3)过点P(m,0)作x轴的垂线(1≤m≤2),分别交平移前后的抛物线于点E,F,交直线OC于点G,求证:PF=EG.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活成为人们的共识,某企业采用技术革新,节能减排,经分析前5个月二氧化碳排放量y(吨)与月份x(月)之间的函数关系是y=-2x+50.
(1)随着二氧化碳排放量的减少,每排放一吨二氧化碳,企业相应获得的利润也有所提高,且相应获得的利润p(万元)与月份x(月)的函数关系如图所示,那么哪月份,该企业获得的月利润最大?最大月利润是多少万元?
(2)受国家政策的鼓励,该企业决定从6月份起,每月二氧化碳排放量在上一个月的基础上都下降a%,与此同时,每排放一吨二氧化碳,企业相应获得的利润在上一个月的基础上都增加50%,要使今年6、7月份月利润的总和是今年5月份月利润的3倍,求a的值(精确到个位).
(参考数据: =7.14,
=7.14, =7.21,
=7.21, =7.28,
=7.28,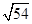 =7.35)
=7.35)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
平面直角坐标中,对称轴平行于y轴的抛物线经过原点O,其顶点坐标为(3,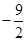 );Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(
);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为( ,0),且BC=5,AC=3(如图1).
,0),且BC=5,AC=3(如图1).
图1 图2
(1)求出该抛物线的解析式;
(2)将Rt△ABC沿x轴向右平移,当点A落在(1)中所求抛物线上时Rt△ABC停止移动.D(0,4)为y轴上一点,设点B的横坐标为m,△DAB的面积为s.
①分别求出点B位于原点左侧、右侧(含原点O)时,s与m之间的函数关系式,并写出相应自变量m的取值范围(可在图1、图2中画出探求);
②当点B位于原点左侧时,是否存在实数m,使得△DAB为直角三角形?若存在,直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com