观察图（1），容易发现图（2）中的∠1=∠2+∠3．把图（2）推广到图（3），其中有8个角：∠1，∠2，…，∠8．可以验证∠1=∠2+∠5+∠8成立．除此之外，恰好还有一组正整数x，y，z，满足2≤x≤y≤z≤8，使得∠1=∠x+∠y+∠z，那么这组正整数（x，y，z）=（　　）

A．（3，4，7）

B．（3，5，7）

C．（3，3，7）

D．（4，6，7）

分析：利用三角形外角的性质及边长为1的正方形网格的性质得到和等于45°的3个角的即可得到答案．

解答：解：∵小正方形的边长为1，
∴∠1=45°，
∵∠1=∠x+∠y+∠z，
∴x+y+z=45，
∵一组正整数x，y，z，满足2≤x≤y≤z≤8，
∴∠1=∠3+∠4+∠7=45°，
∴这组正整数（x，y，z）=3，4，7；
故选A．

点评：本题考查了图形规律类题目，解题的关键是仔细地观察题目提供的例子并从中找到正确的规律，并利用此规律解题．

练习册系列答案

1加1阅读好卷系列答案

相关习题

科目：初中数学 来源： 题型：

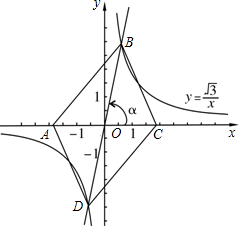我们容易发现：反比例函数的图象是一个中心对称图形．你可以利用这一结论解决问题．如图，在同一直角坐标系中，正比例函数的图象可以看作是：将x轴所在的直线绕着原点O逆时针旋转α度角后的图形．若它与反比例函数y=

的图象分别交于第一、三象限的点B，D，已知点A（-m，O）、C（m，0）．
（1）直接判断并填写：不论α取何值，四边形ABCD的形状一定是

；
（2）①当点B为（p，1）时，四边形ABCD是矩形，试求p，α，和m的值；
②观察猜想：对①中的m值，能使四边形ABCD为矩形的点B共有几个？（不必说理）
（3）试探究：四边形ABCD能不能是菱形？若能，直接写出B点的坐标，若不能，说明理由．

科目：初中数学 来源： 题型：

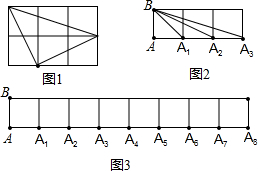（∠AA₁B简写做∠i）观察图1，容易发现图2中的∠1=∠2+∠3．把图2推广到图3，其中有8个角：∠1，∠2，∠3，…，∠8．可以验证∠1=∠2+∠5+∠8成立．除此之外，恰好还有一组正整数x，y，z，满足2≤x≤y≤z≤8，使得∠1=∠x+∠y+∠z，那么这组正整数（x，y，z）=

．

科目：初中数学 来源： 题型：

电焊工想利用一块边长为的正方形钢板做成一个扇形，于是设计了以下三种方案：

方案一：如图1，直接从钢板上割下扇形．

方案二：如图2，先在钢板上沿对角线割下两个扇形，再焊接成一个大扇形（如图3）．

方案三：如图4，先把钢板分成两个相同的小矩形，并在每个小矩形里割下两个小扇形，然后将四个小扇形按与图3类似的方法焊接成一个大扇形．

图1 图2 图3 图4

1.（1）容易得出图1、图3中所得扇形的圆心角均为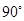，那么按方案三所焊接成的大扇形的圆心角也为吗？为什么？

2.（2）容易得出图1中扇形与图3中所得大扇形的面积相等，那么按方案三所焊成的大扇形的面积也与方案二所焊接成的大扇形的面积相等吗？若不相等，面积是增大还是减小？为什么？

3.（3）若将正方形钢板按类似图4的方式割成个相同的小矩形，并在每个小矩形里割下两个小扇形，然后将这个小扇形按类似方案三的方式焊接成一个大扇形，则当逐渐增大时，所焊接成的大扇形的面积如何变化？

科目：初中数学 来源： 题型：填空题

（∠AA₁B简写做∠i）观察图1，容易发现图2中的∠1=∠2+∠3．把图2推广到图3，其中有8个角：∠1，∠2，∠3，…，∠8．可以验证∠1=∠2+∠5+∠8成立．除此之外，恰好还有一组正整数x，y，z，满足2≤x≤y≤z≤8，使得∠1=∠x+∠y+∠z，那么这组正整数（x，y，z）=________．

同步练习册答案