
【题目】已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点. 
(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值.
【答案】
(1)解:正方形ABCD中,
∵AD=AB,∠ADC=∠ABC=90°,
∴∠ADF=∠ABE=90°,
在△ADF与△ABE中,
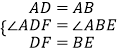 ,
,
∴△ADF≌△ABE
(2)解:过点A作AH⊥DE于点H,
在Rt△ABE中,∵AB=BC=3,
∵BE=1,
∴AE= ![]() ,ED=
,ED= ![]() =5,
=5,
∵S△AED= ![]() AD×BA=
AD×BA= ![]() ,
,
S△ADE= ![]() ED×AH=
ED×AH= ![]() ,
,
解出AH=1.8,
在Rt△AHE中,EH=2.6,
∴tan∠AED= ![]() .
.
【解析】(1)根据辅助线的性质得到AD=AB,∠ADC=∠ABC=90°,由邻补角的定义得到∠ADF=∠ABE=90°,于是得到结论;(2)过点A作AH⊥DE于点H,根据勾股定理得到AE= ![]() ,ED=
,ED= ![]() =5,根据三角形的面积S△AED=
=5,根据三角形的面积S△AED= ![]() AD×BA=
AD×BA= ![]() ,S△ADE=
,S△ADE= ![]() ED×AH=
ED×AH= ![]() ,求得AH=1.8,由三角函数的定义即可得到结论.本题考查了正方形的性质,全等三角形的判定和性质,三角形的面积倒计时,勾股定理,熟练掌握正方形的性质是解题的关键.
,求得AH=1.8,由三角函数的定义即可得到结论.本题考查了正方形的性质,全等三角形的判定和性质,三角形的面积倒计时,勾股定理,熟练掌握正方形的性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】平行四边形的一边长是9cm,那么这个平行四边形的两条对角线的长可以是( )
A. 4cm和6cm B. 6cm和8cm C. 8cm和10cm D. 10cm和12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是边AC上一点,BC=BD=AD,则∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义,我们把对角线互相垂直的四边形叫做垂美四边形.
概念理解:如图②,在四边形ABCD中,如果AB=AD,CB=CD,那么四边形ABCD是垂美四边形吗?请说明理由.
性质探究:如图①,垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系?写出你的猜想,并给出证明.
问题解决:如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连结CE、BG、GE.若AC=2,AB=5,则①求证:△AGB≌△ACE;
②GE= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( ) 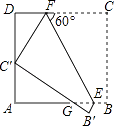
A.3 ![]() ﹣4
﹣4
B.4 ![]() ﹣5
﹣5
C.4﹣2 ![]()
D.5﹣2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于( ) 
A.1
B.2
C.4
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com