
如图,在梯形ABCD中,AB∥CD,∠ABD=90°,AB=BD,在BC上截取BE,使BE=BA,过点B作BF⊥BC于B,交AD于点F.连接AE,交BD于点G,交BF于点H.
(1)已知AD=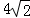 ,CD=2,求sin∠BCD的值;
,CD=2,求sin∠BCD的值;
(2)求证:BH+CD=BC.

(1)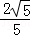 (2)见解析
(2)见解析
【解析】
试题分析:(1)在直角三角形BCD中利用锐角三角函数的定义求解即可;
(2)过点A作AB的垂线交BF的延长线于M,利用全等三角形的判定与性质及等腰直角三角形的性质求解即可.
(1)解:在Rt△ABD中,∠ABD=90°,AB=BD,AD=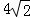 ,
,
则AB=BD=4,…(1分)
在Rt△CBD中,∠BDC=90°,CD=2,BD=4,
所以BC= ,…(2分)
,…(2分)
sin∠BCD=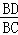 =
=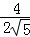 =
=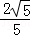 .…(4分)
.…(4分)
(2)证明:过点A作AB的垂线交BF的延长线于M.

∵∠DBA=90°,∴∠1+∠3=90°.
∵BF⊥CB于B,∴∠3+∠2=90°.
∴∠2=∠1.…(5分)
∵BA=BD,∠BAM=∠BDC=90°,
∴△BAM≌△BDC.
∴BM=BC,AM=CD.…(7分)
∵EB=AB,∴∠7=∠5.
BH=BG.…(8分)
∴∠4=∠1+∠5=∠2+∠7=∠6.
∵∠8=∠4,∠MAH=∠6,
∴∠8=∠MAH,∴AM=MH=CD.…(9分)
∴BC=BM=BH+HM=BH+CD. …(10分)
其他解法,参照给分.
点评:本题考查梯形、全等三角形的判定与性质及等腰直角三角形的知识,是一道小的综合题,注意对这些知识的熟练掌握和灵活运用.


科目:初中数学 来源: 题型:
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com