
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.
(1) 求证: AC平分∠DAB;
(2) 若点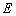 为
为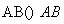 的中点,
的中点, 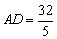 ,AC=8,
,AC=8,
求AB和AE的长.
 |
科目:初中数学 来源: 题型:
一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向向上平行前进,那么两次拐弯的角度是( )
A、第一次右拐50°,第二次左拐130° B、第一次左拐50°, 第二次右拐50°
第二次右拐50°
C、第一次左拐50°,第二次左拐130° D、第一次右拐50°,第二次右拐50°
查看答案和解析>>
科目:初中数学 来源: 题型:
问题情境:
如图1,P是⊙O外的一点,直线PO分别交⊙O于点A、B,则PA是点P到⊙O上的点的最短距离.
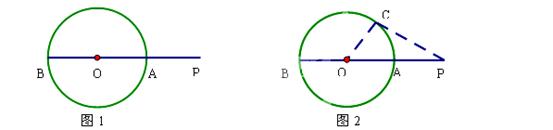
探究:
请您结合图2给予证明,
归纳:
圆外一点到圆上各点的最短距离是:这点到连接这点与圆心连线与圆交点之间的距离.
图中有圆,直接运用:
如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是 上的一个动点,连接AP,则AP的最小值是 .
上的一个动点,连接AP,则AP的最小值是 .

|
图中无圆,构造运用:
如图4,在边长为2的菱形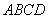 中,∠
中,∠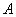 =60°,
=60°, 是
是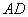 边的中点,
边的中点, 是
是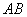 边上一动点,将△
边上一动点,将△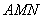 沿
沿 所在的直线翻折得到△
所在的直线翻折得到△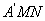 ,连接
,连接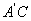 ,请求出
,请求出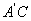 长度的最小
长度的最小
值.

 | |||
|
解:由折叠知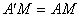 ,又M是AD的中点,可得
,又M是AD的中点,可得 ,故点
,故点 在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
迁移拓展,深化运用:
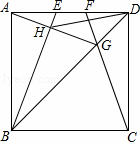
如图6,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
|
查看答案和解析>>
科目:初中数学 来源: 题型:
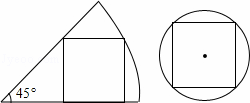
一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是--------( )
|
| A. | 5:4 | B. | 5:2 | C. |
| D. |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com