
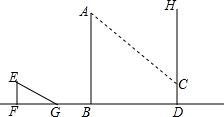
 如图,一根长2m的木棒EF在地面上的影子FG为3m,此时15m高的旗杆AB的影子有一部分恰好落在16m的墙DH上,求旗杆的影子在墙上的高CD的长是多少?(精确到0.1m)
如图,一根长2m的木棒EF在地面上的影子FG为3m,此时15m高的旗杆AB的影子有一部分恰好落在16m的墙DH上,求旗杆的影子在墙上的高CD的长是多少?(精确到0.1m) 分析 延长AC交BD于M,如图,利用“在同一时刻物高与影长的比相等”得到$\frac{EF}{FG}$=$\frac{AB}{BM}$,于是可计算出BM=22.5,则DM=BM-BD=6.5,再证明△MCD∽△MAB,然后利用相似比可计算出CD.
解答 解:延长AC交BD于M,如图,
EF=2m,FG=3m,AB=15m,BD=16m,
∵$\frac{EF}{FG}$=$\frac{AB}{BM}$,即$\frac{2}{3}$=$\frac{15}{BM}$,
∴BM=22.5,
∴DM=BM-BD=22.5-16=6.5,
∵CD∥AB,
∴△MCD∽△MAB,
∴$\frac{CD}{AB}$=$\frac{DM}{BM}$,即$\frac{CD}{15}$=$\frac{6.5}{22.5}$,
∴CD≈4.4(m).
答:旗杆的影子在墙上的高CD的长是4.4m.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果a<b,那么a-c<b-c | B. | 如果a>b,c>0,那么ac>bc | ||
| C. | 如果m<n,p<0,那么$\frac{m}{p}$>$\frac{n}{p}$ | D. | 如果x>y,z<0,那么xz>yz |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm,2cm,4cm | B. | 4cm,5cm,9cm | C. | 5cm,8cm,15cm | D. | 6cm,8cm,9cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com