
已知m2﹣mn=2,mn﹣n2=5,则3m2+2mn﹣5n2=__________
31
【考点】因式分解的应用;代数式求值.
【专题】计算题.
【分析】结合已知等式,分别将原式中的m2和n2代换,再进行化简即可得出最终结果.
【解答】解:方法一:
根据题意,m2﹣mn=2,mn﹣n2=5,故有m2=2+mn,n2=mn﹣5,
∴原式=3(2+mm)+2mn﹣5(mn﹣5)=31.
故应填31.
方法二:根据已知条件m2﹣mn=2,mn﹣n2=5,得
m(m﹣n)=2,n(m﹣n)=5
∴两式相加得,(m+n)(m﹣n)=7,m+n=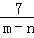
∴3m2+2mn﹣5n2=3(m+n)(m﹣n)+2n(m﹣n)
=3(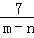 )(m﹣n)+2(
)(m﹣n)+2(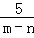 )(m﹣n)
)(m﹣n)
=21+10
=31.
故应填31.
【点评】本题主要考查整体代换的思想来求解代数式的问题,属于常考题目,希望学生能够熟练掌握和应用.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com