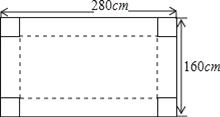
【题目】我国水资源比较缺乏，人均水量约为世界人均水量的四分之一，其中西北地区缺水尤为严重．一村民为了蓄水，他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水．已知白铁皮的长为280cm，宽为160cm（如图）．
（1）若水箱的底面积为16000cm2，请求出切去的小正方形边长；
（2）对（1）中的水箱，若盛满水，这时水量是多少升？（注：1升水=1000cm3水）
【答案】（1）切去的小正方形边长为40cm；（2）这时水量为640升．
【解析】试题分析：（1）设切去的小正方形的边长为xcm，然后用含x的式子表示水箱底面的长和宽，然后依据矩形的面积公式列方程求解即可；
（2）依据正方体的体积=底面积×高求得水的体积，然后再依据1升水=1000cm3水求解即可．
试题解析：（1）设切去的小正方形的边长为xcm．
根据题意，得：=16000，
化简整理，得：x2﹣220x+7200=0，
解得x=40或x=180（舍去），
答：切去的小正方形边长为40cm；
（2）在（1）的条件下，水箱的容积=16000×40=640000cm3，
640000÷1000=640（升），
答：这时水量为640升．
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO.若∠COB＝60°，FO＝FC，则下列结论：①FB⊥OC，OM＝CM；②△EOB≌△CMB；③四边形EBFD是菱形；④MB∶OE＝3∶2.其中正确结论的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一水果商某次按每千克3.2元购进一批苹果，销售过程中有20%的苹果正常损耗，为避免亏本，该水果商应将这批苹果的售价至少定为每千克_____元．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线的顶点坐标为C（0，8），并且经过A（8，0），点P是抛物线上点A，C间的一个动点（含端点），过点P作直线y=8的垂线，垂足为点F，点D，E的坐标分别为（0，6），（4，0），连接PD，PE，DE．
（1）求抛物线的解析式；
（2）猜想并探究：对于任意一点P，PD与PF的差是否为固定值？如果是，请求出此定值；如果不是，请说明理由；
（3）求：①当△PDE的周长最小时的点P坐标；②使△PDE的面积为整数的点P的个数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图①是某手机生产厂第一季度三个月产量统计图，图②是这三个月的产量与第一季度总产量的比例分布统计图，统计员在制作图①、图②时漏填了部分数据．
（1）该厂二月份生产的手机产量占第一季度的比例为 %；
（2）求该厂三月份生产手机的产量；
（3）请求出图②中一月份圆心角的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
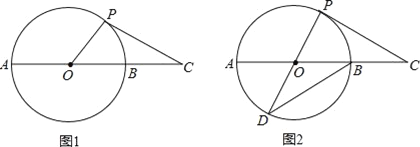
【题目】如图1，延长⊙O的直径AB至点C，使得BC=
AB，点P是⊙O上半部分的一个动点（点P不与A、B重合），连结OP，CP．
（1）∠C的最大度数为 ；
（2）当⊙O的半径为3时，△OPC的面积有没有最大值？若有，说明原因并求出最大值；若没有，请说明理由；
（3）如图2，延长PO交⊙O于点D，连结DB，当CP=DB时，求证：CP是⊙O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有长为24m的篱笆，围成中间隔有一道篱笆的长方形的花圃，且花圃的长可借用一段墙体(墙体的最大可用长度a＝10m)．
(1)如果所围成的花圃的面积为45m2，试求宽AB的长；
(2)按题目的设计要求，能围成面积比45m2更大的花圃吗?如果能，请求出最大面积，并说明围法；如果不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平行四边形ABCD中，AB⊥AC，AB=1，BC=
．对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F．
（1）证明：当旋转角为90°时，四边形ABEF是平行四边形；
（2）试说明在旋转过程中，线段AF与EC总保持相等；
（3）在旋转过程中，四边形BEDF可能是菱形吗？如果不能，请说明理由；如果能，说明理由并求出此时AC绕点O顺时针旋转的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com