
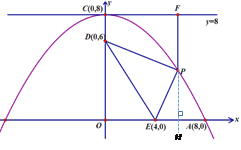
【题目】如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值?如果是,请求出此定值;如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.

【答案】(1)抛物线的解析式为y=﹣![]() x2+8;(2)PD与PF的差是定值,PD﹣PF=2;(3)①P(4,6),此时△PDE的周长最小;②共有11个令S△DPE为整数的点.
x2+8;(2)PD与PF的差是定值,PD﹣PF=2;(3)①P(4,6),此时△PDE的周长最小;②共有11个令S△DPE为整数的点.
【解析】(1)设抛物线的解析式为y=a(x+h)2+k
∵点C(0,8)是它的顶点坐标, ∴y=ax2+8
又∵经过点A(8,0),
有64a+8=0,解得a=![]()
故抛物线的解析式为:y=![]() x2+8;
x2+8;
(2)是定值,解答如下:
设P(a,![]() a2+8),则F(a,8),
a2+8),则F(a,8),
∵D(0,6),
∴PD=![]()
PF=![]() ,
,
∴PD﹣PF=2;
(3)当点P运动时,DE大小不变,则PE与PD的和最小时,△PDE的周长最小,
∵PD﹣PF=2,∴PD=PF+2,
 ∴PE+PD=PE+PF+2,
∴PE+PD=PE+PF+2,
∴当P、E、F三点共线时,PE+PF最小,
此时点P,E的横坐标都为4,
将x=4代入y=![]() x2+8,得y=6,
x2+8,得y=6,
∴P(4,6),此时△PDE的周长最小.
过点P做PH⊥x轴,垂足为H.
设P(a,![]() a2+8)
a2+8)
∴PH=![]() a2+8,EH=a-4,OH=a
a2+8,EH=a-4,OH=a
S△DPE=S梯形PHOD-S△PHE-S△DOE
=![]()
=![]()
=![]()
∵点P是抛物线上点A,C间的一个动点(含端点)
∴0≤a≤8
当a=6时,S△DPE取最大值为13.
当a=0时,S△DPE取最小值为4.
即4≤S△DPE≤13
其中,当S△DPE=12时,有两个点P.
所以,共有11个令S△DPE为整数的点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某小区为更好的提高业主垃圾分类的意识,管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和4个垃圾箱共需580元,且每个温馨提示牌比垃圾箱便宜40元.
(1)问购买1个温馨提示牌和1个垃圾箱各需多少元?
(2)如果需要购买温馨提示牌和垃圾箱共100个,费用不超过8000元,问最多购买垃圾箱多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.
(1)利用尺规,以AB为直径作⊙O,交BC于点D;(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,求证:AC2=CDCB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
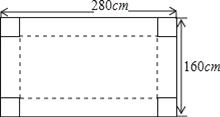
【题目】我国水资源比较缺乏,人均水量约为世界人均水量的四分之一,其中西北地区缺水尤为严重.一村民为了蓄水,他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水.已知白铁皮的长为280cm,宽为160cm(如图).
(1)若水箱的底面积为16000cm2,请求出切去的小正方形边长;
(2)对(1)中的水箱,若盛满水,这时水量是多少升?(注:1升水=1000cm3水)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com