练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△ABC中，∠BAC=90°，AB=AC．

    （1）利用尺规，以AB为直径作⊙O，交BC于点D；（保留作图痕迹，不写作法）

    （2）在（1）所作的图形中，求证：AC2=CDCB．

    【答案】（1）作图见解析；（2）证明见解析.

    【解析】试题分析：（1）作AB的垂直平分线得到AB的中点O，然后以O为圆心，OA为半径作圆交BC于D；

    （2）先利用圆周角定理得到∠ADB=∠CAB，则可判断△CAD∽△CBA，然后利用相似比得到CA：CB=CD：CA，再根据比例的性质即可得到结论．

    试题解析：（1）如图所示：

    （2）连接AD，如图，

    ∵AB是直径，∴∠ADB=90°，∴∠ADB=∠CAB，

    ∵∠C=∠C，∴△CAD∽△CBA，∴CA：CB=CD：CA，

    ∴AC2=CDCB．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在正三角形、等腰梯形、矩形、平行四边形中，既是轴对称图形又是中心对称图形的是（ ）
    A.正三角形
    B.等腰梯形
    C.矩形
    D.平行四边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解下列关于x的不等式（组）：

    （1） （2）

    （3） （4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO.若∠COB＝60°，FO＝FC，则下列结论：①FB⊥OC，OM＝CM；②△EOB≌△CMB；③四边形EBFD是菱形；④MB∶OE＝3∶2.其中正确结论的个数是（ ）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知m＋n＝2，mn＝－2，则(2－m)(2－n)的值为(　　)

    A. 2 B. －2 C. 0 D. 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一水果商某次按每千克3.2元购进一批苹果，销售过程中有20%的苹果正常损耗，为避免亏本，该水果商应将这批苹果的售价至少定为每千克_____元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线的顶点坐标为C（0，8），并且经过A（8，0），点P是抛物线上点A，C间的一个动点（含端点），过点P作直线y=8的垂线，垂足为点F，点D，E的坐标分别为（0，6），（4，0），连接PD，PE，DE．

    （1）求抛物线的解析式；

    （2）猜想并探究：对于任意一点P，PD与PF的差是否为固定值？如果是，请求出此定值；如果不是，请说明理由；

    （3）求：①当△PDE的周长最小时的点P坐标；②使△PDE的面积为整数的点P的个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

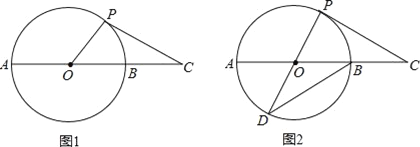
    【题目】如图1，延长⊙O的直径AB至点C，使得BC=AB，点P是⊙O上半部分的一个动点（点P不与A、B重合），连结OP，CP．

    （1）∠C的最大度数为 　；

    （2）当⊙O的半径为3时，△OPC的面积有没有最大值？若有，说明原因并求出最大值；若没有，请说明理由；

    （3）如图2，延长PO交⊙O于点D，连结DB，当CP=DB时，求证：CP是⊙O的切线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】月初，明斯克航母告别盐田，据不完全估算，16年间累计接待游客11000000人次，11000000用科学记数法表示是 ．

    查看答案和解析>>

    同步练习册答案