
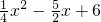 的图象与x轴从左到右的两个交点依次为A、B,与y轴交点为C;
的图象与x轴从左到右的两个交点依次为A、B,与y轴交点为C; 解:(1)由题意,在y=
解:(1)由题意,在y= x2-
x2- 中,令x=0及y=0
中,令x=0及y=0 ,
,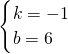 ;
; ×4×y,
×4×y, BC=
BC=
 =3
=3 =
= ,
, >4;
>4; (即
(即 ),显然这个距离要大于4,因此P点的坐标无论去何值,都不存在OP=OA的情况.
),显然这个距离要大于4,因此P点的坐标无论去何值,都不存在OP=OA的情况.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013年浙江省杭州市西湖区中考一模数学试卷(带解析) 题型:解答题
已知:二次函数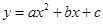
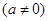 中的
中的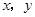 满足下表:
满足下表:
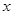 | |  | 0 | 1 | 2 | 3 | |
 | | 0 | 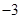 | 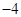 | 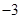 | 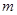 | |
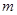 的值;
的值;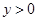 时的
时的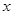 的取值范围;
的取值范围;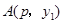 ,
, 两点都在该函数图象上,且
两点都在该函数图象上,且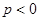 ,试比较
,试比较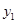 与
与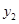 的大小.
的大小.查看答案和解析>>
科目:初中数学 来源:2007年上海市普陀区中考数学二模试卷(解析版) 题型:解答题
 的图象与x轴相交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,图象与y轴交于点C,OB=2OA;
的图象与x轴相交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,图象与y轴交于点C,OB=2OA; 与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M′、N′,点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q,是否存在t值,使S梯形MM'N'N:S△QMN=35:12?若存在,求出满足条件的t值;若不存在,请说明理由.
与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M′、N′,点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q,是否存在t值,使S梯形MM'N'N:S△QMN=35:12?若存在,求出满足条件的t值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:1999年全国中考数学试题汇编《二次函数》(02)(解析版) 题型:解答题
 的图象与x轴从左到右的两个交点依次为A、B,与y轴交点为C;
的图象与x轴从左到右的两个交点依次为A、B,与y轴交点为C;查看答案和解析>>
科目:初中数学 来源:2012年浙教版初中数学九年级上2.1二次函数练习卷(解析版) 题型:选择题
已知:二次函数 中的x、y满足下表:
中的x、y满足下表:
|
|
… |
|
0 |
1 |
2 |
3 |
… |
|
|
… |
0 |
|
|
|
|
… |
m的值为( )
A.-2 B.5 C.1 D.0
查看答案和解析>>
科目:初中数学 来源:2012-2013学年上海市闸北区中考一模数学试卷(解析版) 题型:解答题
(本题满分10分 第(1)小题4分,第(2)小题6分)
已知:二次函数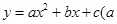 ≠0的图像经过点(3,5)、(2,8)、(0,8).
≠0的图像经过点(3,5)、(2,8)、(0,8).
(1)求这个二次函数的解析式;
(2)已知抛物线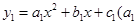 ≠0,
≠0,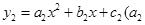 ≠0,且满足
≠0,且满足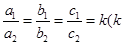 ≠0,1,则我们称抛物线
≠0,1,则我们称抛物线 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当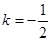 时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com