
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
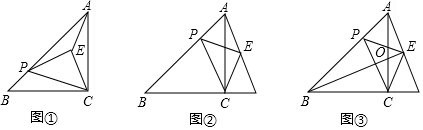
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,双曲线y1=$\frac{{k}_{1}}{x}$(x<0)经过A(-2,3),双曲线y2=$\frac{{k}_{2}}{x}$(x2>0)经过C点,D点在y轴正半轴上,B(1,0)点在x轴的正半轴上,若四边形ABCD是矩形.
如图,双曲线y1=$\frac{{k}_{1}}{x}$(x<0)经过A(-2,3),双曲线y2=$\frac{{k}_{2}}{x}$(x2>0)经过C点,D点在y轴正半轴上,B(1,0)点在x轴的正半轴上,若四边形ABCD是矩形.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:填空题
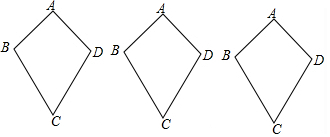
一机器人以0.3m/s的速度在平地上按下图中的步骤行走,那么该机器人从开始到停止所需时间为__s.

查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省泉州市泉港区七年级3月教学质量检测数学试卷(解析版) 题型:解答题
某玩具工厂出售一种玩具,其成本价每件28元.如果直接由厂家门市部销售,每件产品售价为35元,同时每月还要支出其他费用2100元;如果委托商场销售,那么出厂价为32元.
(1)求在两种销售方式下,每个月销售多少件时,所得利润相等?
(2)若每个月销售量达到1000件时,采用哪种销售方式获得利润较多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com