
��ͼ��ʾ,ij����С��Ҫ��һ��һ�߿�ǽ��ǽ��15m���Ŀյ�����һ�����λ�ABCD,����һ�߿�ǽ,���������ܳ�Ϊ40m��դ��Χ��,������BC�߳�Ϊx��,�������Ϊy��m2��
��1����y��x֮��ĺ�����ϵʽ,��д���Ա���x��ȡֵ��Χ;
��2�����������Ļ�����ܴﵽ200m2������,�����ʱx��ֵ;������,˵������;
��3����������,�жϵ�xȡ��ֵʱ,����������
��1��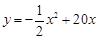 ��0��x��15��;
��0��x��15��;
��2����������ܴﵽ200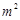 ,���ɼ�����;
,���ɼ�����;
��3����x=15ʱ,��������
���������������1����֪���εij����ܳ��ɱ�ʾ��,���ù�ʽ��ʾ���,����ǽ����x��ȡֵ��Χ;
��2����y=200ʱx��ֵ,�����Ա�����ȡֵ��Χ�ش�����;
��3�����ݺ�����ϵʽ������������ֵ��
�����������1����������ã�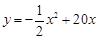 ��0��x��15��
��0��x��15��
��2������
��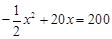 ,��ã�
,��ã�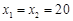 ��15,
��15,
�������ܴﵽ200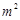 ;
;
��3����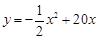 =
=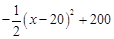
�ຯ��ͼ��Ϊ��20,200���ҿ�������,�൱x��20ʱ,
y��x�����������,��0��x��15
�൱x=15ʱ,y���,��x=15mʱ,��������
���㣺���κ�����Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ƽ��ֱ������ϵxOy�У����κ��� ��ͼ���A��-1��-2����B��1��0�����㣮
��ͼ���A��-1��-2����B��1��0�����㣮
��1����˶��κ����Ľ���ʽ���������κ���ͼ��
��2����P(t,0)��x���ϵ�һ�����㣬����P��x��Ĵ��߽�ֱ��AB�ڵ�M�������κ�����ͼ���ڵ�N������Mλ�ڵ�N���Ϸ�ʱ��ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ƽ��ֱ������ϵxOy�У�������y=ax2-4ax+4a+c ��x�ύ�ڵ�A��B����y��������ύ�ڵ�C����A������Ϊ��1��0����OB=OC.
��x�ύ�ڵ�A��B����y��������ύ�ڵ�C����A������Ϊ��1��0����OB=OC.
��1����������ߵĽ���ʽ��
��2������P���߶�BC�ϵ�һ�����㣬����P��y���ƽ��������������x���·����ڵ�Q�������߶�PQ�ij����Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
��3�����������ߵĶԳ����ϵĵ�M�����AMC=45�㣬���M������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У��߳�Ϊ2��������OABC�Ķ���A��C�ֱ���x�ᡢy����������ϣ����κ���y=- x2+bx+c��ͼ��B��C���㣮
x2+bx+c��ͼ��B��C���㣮
��1����b��c��ֵ��
��2����Ϻ�����ͼ��̽������y��0ʱx��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�߿Ƽ���չ��˾Ͷ��500��Ԫ���ɹ����Ƴ�һ���г��������ϴ�ĸ߿Ƽ������Ʒ����Ͷ���ʽ�1500��Ԫ��Ϊ�̶�Ͷ�ʣ���֪����ÿ����Ʒ�ijɱ���40Ԫ�������۹����з��֣������۵��۶�Ϊ100Ԫʱ����������Ϊ20��������۵���ÿ����10Ԫ����������������1����������۵���Ϊx��Ԫ������������Ϊy���������������������=�����۶�һ�����ɱ���Ͷ�ʣ�Ϊz����Ԫ����
��1����д��y��x֮��ĺ�����ϵʽ����дx��ȡֵ��Χ����
��2����д��z��x֮��ĺ�����ϵʽ����дx��ȡֵ��Χ����
��3����˾�ƻ����ڵ�һ�갴��������ȷ�����۵��۽������ۣ����ڶ��������������1130��Ԫ������������Ĵ���ͼ��˵�����ڶ�������۵���x��Ԫ��Ӧȷ����ʲô��Χ�ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪������y=x2+bx+c������2����1���ͣ�4,3�����㣮
(1)�����������ߵĽ���ʽ��
(2)��������������ƽ��1����λ��������ƽ��3����λ���õ����������߽���ʽΪ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�����κ��� ��ͼ����һ�κ���
��ͼ����һ�κ��� ��ͼ����
��ͼ���� ��
�� ����. C
����. C Ϊ���κ���ͼ��Ķ���.
Ϊ���κ���ͼ��Ķ���.
��1������κ��� �Ľ���ʽ��
�Ľ���ʽ��
��2�����庯��f�������Ա���x��ȡһֵʱ��x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2����y1��y2������f�ĺ���ֵ����y1��y2�еĽ�Сֵ;��y1=y2������f�ĺ���ֵ����y1����y2��.�� ��ֱ�� ��k >0���뺯��f��ͼ��ֻ����������ʱ����
��k >0���뺯��f��ͼ��ֻ����������ʱ���� ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪�������� ��x�ύ�ڵ�A��B��A��B�ң������е�B������Ϊ��7��0�����������ߵĶ���ΪC��
��x�ύ�ڵ�A��B��A��B�ң������е�B������Ϊ��7��0�����������ߵĶ���ΪC��
��1���������ߵĽ���ʽ�͵�C�����ꣻ
��2����ͼ1����AC��y���ڵ�D����D����DE��AB��BC��E����PΪDE��һ���㣬PF��AC��F��PG��BC��G�����P�ĺ�����Ϊa���ı���CFPG�����Ϊy����y��a�ĺ�����ϵʽ��y�����ֵ��
��3����ͼ2����������2���£���P��PH��x���ڵ�H������FH��GH���Ƿ���ڵ�P��ʹ�á�PFH���PHG���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��������y=ax2+bx+c������A����3��0����B��0��3����C��1��0����
��1����������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ�����������һ���㣬�������A��B�غϣ�������P��x��Ĵ��ߣ�����ΪF����ֱ��AB�ڵ�E����PD��AB�ڵ�D��
�ٶ���P��ʲôλ��ʱ����PDE���ܳ���������ʱP������ꣻ
������PA����APΪ����ͼʾһ���������APMN�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣮
������M��Nǡ�����������߶Գ�����ʱ�������Ӧ��P������꣮������������ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com