
已知抛物线y=x2+bx+c经过(2,-1)和(4,3)两点.
(1)求出这个抛物线的解析式;
(2)将该抛物线向右平移1个单位,再向下平移3个单位,得到的新抛物线解析式为 .
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
如图,二次函数 的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
(1)求二次函数的解析式;
(2)设点D的坐标为(x,y),试求矩形ABCD的周长P关于自变量x的函数解析式,并求出自变量x的取值范围;
(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
二次函数y=ax²-6ax+c(a>0)的图像抛物线过点C(0,4),设抛物线的顶点为D。
(1)若抛物线经过点(1,-6),求二次函数的解析式;
(2)若a=1时,试判断抛物线与x轴交点的个数;
(3)如图所示A、B是⊙P上两点,AB=8,AP=5。且抛物线过点A(x1,y1),B(x2,y2),并有AD=BD。设⊙P上一动点E(不与A、B重合),且∠AEB为锐角,若<a≤1时,请判断∠AEB与∠ADB的大小关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,若花园的BC边长为x米,花园的面积为y(m2)
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)满足条件的花园面积能达到200m2吗?若能,求出此时x的值;若不能,说明理由;
(3)请结合题意,判断当x取何值时,花园的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数 .
.
(1)若点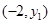 与
与 在此二次函数的图象上,则
在此二次函数的图象上,则
 (填 “>”、“=”或“<”);
(填 “>”、“=”或“<”);
(2)如图,此二次函数的图象经过点 ,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,
与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C, ,且S△AOC=1,过点P作PB⊥y轴于点B.
,且S△AOC=1,过点P作PB⊥y轴于点B.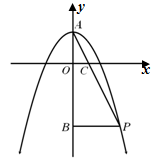
(1)求BP的长;
(2)求抛物线与x轴的交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com