
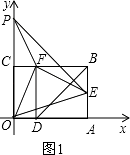
ΓΨΧβΡΩΓΩ»γΆΦΘ§“‘ΨΊ–ΈOABCΒΡΕΞΒψOΈΣ‘≠ΒψΘ§OAΥυ‘ΎΒΡ÷±œΏΈΣx÷αΘ§OCΥυ‘ΎΒΡ÷±œΏΈΣy÷αΘ§Ϋ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ°“―÷ΣOA=3Θ§OC=2Θ§ΒψE «ABΒΡ÷–ΒψΘ§‘ΎOA…œ»Γ“ΜΒψDΘ§ΫΪΓςBDA―ΊBDΖ≠’έΘ§ ΙΒψA¬δ‘ΎBC±Ώ…œΒΡΒψF¥ΠΘ°
Θ®1Θ©÷±Ϋ”–¥≥ωΒψEΓΔFΒΡΉχ±ξΘΜ
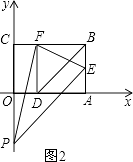
Θ®2Θ©…ηΕΞΒψΈΣFΒΡ≈ΉΈοœΏΫΜy÷α’ΐΑκ÷α”ΎΒψPΘ§«““‘ΒψEΓΔFΓΔPΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘ§«σΗΟ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®3Θ©‘Ύx÷αΓΔy÷α…œ «ΖώΖ÷±π¥φ‘ΎΒψMΓΔNΘ§ ΙΒΟΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΉν–ΓΘΩ»γΙϊ¥φ‘ΎΘ§«σ≥ω÷ή≥ΛΒΡΉν–Γ÷ΒΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚEΘ®3Θ§1Θ©ΘΜFΘ®1Θ§2Θ©Θ°
Θ®2Θ©ΫβΘΚ‘ΎRtΓςEBF÷–Θ§ΓœB=90ΓψΘ§
ΓύEF= ![]() Θ°
Θ°
…ηΒψPΒΡΉχ±ξΈΣΘ®0Θ§nΘ©Θ§Τδ÷–nΘΨ0Θ§
ΓΏΕΞΒψFΘ®1Θ§2Θ©Θ§
Γύ…η≈ΉΈοœΏΫβΈω ΫΈΣy=aΘ®x©¹1Θ©2+2Θ®aΓΌ0Θ©Θ°
ΔΌ »γΆΦ1Θ§
Β±EF=PF ±Θ§EF2=PF2Θ§
Γύ12+Θ®n©¹2Θ©2=5Θ°
ΫβΒΟn1=0Θ®…α»ΞΘ©ΘΜn2=4Θ°
ΓύPΘ®0Θ§4Θ©Θ°
Γύ4=aΘ®0©¹1Θ©2+2Θ°
ΫβΒΟa=2Θ°
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=2Θ®x©¹1Θ©2+2
ΔΎ »γΆΦ2Θ§
Β±EP=FP ±Θ§EP2=FP2Θ§
ΓύΘ®2©¹nΘ©2+1=Θ®1©¹nΘ©2+9Θ°
ΫβΒΟ ![]() Θ®…α»ΞΘ©
Θ®…α»ΞΘ©
ΔέΒ±EF=EP ±Θ§EP= ![]() Θ§’β÷÷«ιΩω≤Μ¥φ‘ΎΘ°
Θ§’β÷÷«ιΩω≤Μ¥φ‘ΎΘ°
Ήέ…œΥυ ωΘ§ΖϊΚœΧθΦΰΒΡ≈ΉΈοœΏΫβΈω Ϋ «y=2Θ®x©¹1Θ©2+2Θ°
Θ®3Θ©ΫβΘΚ¥φ‘ΎΒψMΘ§NΘ§ ΙΒΟΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΉν–ΓΘ°
»γΆΦ3Θ§ΉςΒψEΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψEΓδΘ§ΉςΒψFΙΊ”Ύy÷αΒΡΕ‘≥ΤΒψFΓδΘ§ 
Ν§Ϋ”EΓδFΓδΘ§Ζ÷±π”κx÷αΓΔy÷αΫΜ”ΎΒψMΘ§NΘ§‘ρΒψMΘ§NΨΆ «Υυ«σΒψΘ°
ΓύEΓδΘ®3Θ§©¹1Θ©Θ§FΓδΘ®©¹1Θ§2Θ©Θ§NF=NFΓδΘ§ME=MEΓδΘ°
ΓύBFΓδ=4Θ§BEΓδ=3Θ°
ΓύFN+NM+ME=FΓδN+NM+MEΓδ=EΓδFΓδ= ![]() Θ°
Θ°
”÷ΓΏ ![]() Θ§
Θ§
ΓύFN+MN+ME+EF=5+ ![]() Θ§¥Υ ±ΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΉν–Γ÷Β «
Θ§¥Υ ±ΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΉν–Γ÷Β « ![]() Θ°
Θ°
ΓΨΫβΈωΓΩΘ®1Θ© Ήœ»“άΨίΖ≠’έΒΡ–‘÷ Ω…÷ΛΟςΥΡ±Ώ–ΈADFB «’ΐΖΫ–ΈΘ§Ι ¥ΥΩ…ΒΟΒΫBF=AB=OC=2Θ§‘ρCF=3-2=1Θ§“ρΕχEΓΔFΒΡΉχ±ξΨΆΩ…“‘«σ≥ωΘΜ
Θ®2Θ©”…≈ΉΈοœΏΒΡΕΞΒψΉχ±ξΈΣΘ®1Θ§2Θ©Θ§Ι ¥ΥΩ……η≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=aΘ®x-1Θ©2+2Θ§»ΜΚσΖ÷ΈΣ“‘œ¬»ΐΫ«–Έ«ιΩωΫχ––Ϋβ¥πΦ¥Ω…ΘΚΒ±EF «―ϋΘ§EF=PF ±Θ§“―÷ΣEΓΔFΒψΒΡΉχ±ξΩ…“‘«σ≥ωEFΒΡ≥ΛΘ§…ηPΒψΒΡΉχ±ξ «Θ®0Θ§nΘ©Θ§ΗυΨίΙ¥Ι…Ε®άμΨΆΩ…“‘«σ≥ωnΒΡ÷ΒΘ°ΒΟΒΫPΒΡΉχ±ξΘ°Β±EF «―ϋΘ§EF=EP ±Θ§Ω…“‘≈–ΕœEΒΫy÷αΒΡΉνΕΧΨύάκ”κEFΒΡ¥σ–ΓΙΊœΒΘ§÷Μ”–Β±EF¥σ”ΎEΒΫy÷αΒΡΨύάκΘ§P≤≈¥φ‘ΎΘ°Β±EF «ΒΉ±Ώ ±Θ§EP=FPΘ§ΗυΨίΙ¥Ι…Ε®άμΨΆΩ…“‘ΒΟΒΫΙΊ”ΎnΒΡΖΫ≥ΧΘ§ΨΆΩ…“‘ΫβΒΟnΒΡ÷ΒΘ°
Θ®3Θ©ΉςΒψEΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψEΓδΘ§ΉςΒψFΙΊ”Ύy÷αΒΡΕ‘≥ΤΒψFΓδΘ§“άΨί÷αΕ‘≥ΤΆΦ–ΈΒΡ–‘÷ Ω…ΒΟΒΫNF=NFΓδΘ§ME=MEΓδΘ§»ΜΚσ“άΨίΝΫΒψ÷°ΦδœΏΕΈΉνΕΧΩ…ΒΟΒΫFN+NM+MEΒΡΉν–Γ÷ΒΒ»”ΎEΓδFΓδΘ§Ι ¥ΥΩ…ΒΟΒΫΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΒΡΉν–Γ÷Β.
ΓΨΩΦΒψΨΪΈωΓΩΫβ¥π¥ΥΧβΒΡΙΊΦϋ‘Ύ”ΎάμΫβΕΰ¥ΈΚ· ΐΒΡΆΦœσΒΡœύΙΊ÷Σ ΕΘ§’ΤΈ’Εΰ¥ΈΚ· ΐΆΦœώΙΊΦϋΒψΘΚ1ΓΔΩΣΩΎΖΫœρ2ΓΔΕ‘≥Τ÷α 3ΓΔΕΞΒψ 4ΓΔ”κx÷αΫΜΒψ 5ΓΔ”κy÷αΫΜΒψΘ§“‘ΦΑΕ‘Εΰ¥ΈΚ· ΐΒΡ–‘÷ ΒΡάμΫβΘ§ΝΥΫβ‘ωΦθ–‘ΘΚΒ±a>0 ±Θ§Ε‘≥Τ÷αΉσ±ΏΘ§yΥφx‘ω¥σΕχΦθ–ΓΘΜΕ‘≥Τ÷α”“±ΏΘ§yΥφx‘ω¥σΕχ‘ω¥σΘΜΒ±a<0 ±Θ§Ε‘≥Τ÷αΉσ±ΏΘ§yΥφx‘ω¥σΕχ‘ω¥σΘΜΕ‘≥Τ÷α”“±ΏΘ§yΥφx‘ω¥σΕχΦθ–ΓΘ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“ –ΙφΜ°÷–Ρ≥ΒΊΕΈΒΊΧζœΏ¬Ζ“Σ¥©‘ΫΜΛ≥«Κ”PQΘ§’ΨΒψAΚΆ’ΨΒψB‘ΎΚ”ΒΡΝΫ≤ύΘ§“Σ≤βΥψ≥ωAΓΔBΦδΒΡΨύάκΘ°ΙΛ≥Χ»Υ‘±‘ΎΒψP¥Π≤βΒΟA‘Ύ’ΐ±±ΖΫœρΘ§BΈΜ”ΎΡœΤΪΕΪ24.5ΓψΖΫœρΘ§«Α––1200mΘ§ΒΫ¥οΒψQ≥ωΘ§≤βΒΟAΈΜ”Ύ±±ΤΪΕΪ49ΓψΖΫœρΘ§BΈΜ”ΎΡœΤΪΈς41ΓψΖΫœρΘ°ΗυΨί“‘…œ ΐΨίΘ§«σAΓΔBΦδΒΡΨύάκΘ°Θ®≤ΈΩΦ ΐΨίΘΚcos41ΓψΓ÷0.75Θ©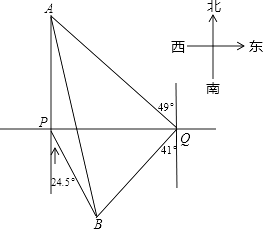
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ”ΟΓΑΓυΓ±Ε®“ε“Μ÷÷–¬‘ΥΥψΘΚΕ‘”Ύ»Έ“β”–άμ ΐaΚΆbΘ§ΙφΕ®aΓυbΘΫab2+2ab+aΘ°
»γΘΚ1Γυ2ΘΫ1ΓΝ22+2ΓΝ1ΓΝ2+1ΘΫ9
Θ®1Θ©Θ®©¹2Θ©Γυ3ΘΫΓΓ ΘΜ
Θ®2Θ©»τ![]() Γυ3ΘΫ16Θ§«σaΒΡ÷ΒΘΜ
Γυ3ΘΫ16Θ§«σaΒΡ÷ΒΘΜ
Θ®3Θ©»τ2ΓυxΘΫmΘ§Θ®![]() xΘ©Γυ3ΘΫnΘ®Τδ÷–xΈΣ”–άμ ΐΘ©Θ§ ‘±»ΫœmΘ§nΒΡ¥σ–ΓΘ°
xΘ©Γυ3ΘΫnΘ®Τδ÷–xΈΣ”–άμ ΐΘ©Θ§ ‘±»ΫœmΘ§nΒΡ¥σ–ΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ’ΐΖΫ–ΈABCDΆβ≤ύΘ§ΉςΒ»±Ώ»ΐΫ«–ΈADEΘ§ACΘ§BEœύΫΜ”ΎΒψFΘ§‘ρΓœBFCΈΣΘ® Θ©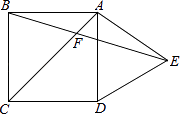
A.75Γψ
B.60Γψ
C.55Γψ
D.45Γψ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐyΘΫΘ®mΘΪ1Θ©x2Θ≠|m|ΘΪnΘΪ4Θ°
Θ®1Θ©Β±mΘ§nΈΣΚΈ÷Β ±Θ§¥ΥΚ· ΐ «“Μ¥ΈΚ· ΐΘΩ
Θ®2Θ©Β±mΘ§nΈΣΚΈ÷Β ±Θ§¥ΥΚ· ΐ «’ΐ±»άΐΚ· ΐΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ’ΐΖΫ–ΈABCDΡΎ”–“Μ’έœΏΕΈΘ§Τδ÷–AE¹AEFΘ§EF¹AFCΘ§≤Δ«“AE=6Θ§EF=8Θ§FC=10Θ§‘ρ’ΐΖΫ–Έ”κΤδΆβΫ”‘≤÷°Φδ–Έ≥…ΒΡ“θ”Α≤ΩΖ÷ΒΡΟφΜΐΈΣ Θ° 
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–ΓΈΡΓΔ–ΓΝΝ¥”―ß–Θ≥ωΖΔΒΫ«ύ…ΌΡξΙ§≤ΈΦ” ιΖ®±»»ϋΘ§–ΓΈΡ≤Ϋ––“ΜΕΈ ±ΦδΚσΘ§–ΓΝΝΤοΉ‘––≥Β―ΊœύΆ§¬ΖœΏ––ΫχΘ§ΝΫ»ΥΨυ‘»ΥΌ«Α––Θ°ΥϊΟ«ΒΡ¬Ζ≥Χ≤νsΘ®ΟΉΘ©”κ–ΓΈΡ≥ωΖΔ ±ΦδtΘ®Ζ÷Θ©÷°ΦδΒΡΚ· ΐΙΊœΒ»γΆΦΥυ ΨΘ°œ¬Ν–ΥΒΖ®ΘΚΔΌ–ΓΝΝœ»ΒΫ¥ο«ύ…ΌΡξΙ§ΘΜΔΎ–ΓΝΝΒΡΥΌΕ» «–ΓΈΡΥΌΕ»ΒΡ2.5±ΕΘΜΔέa=24ΘΜΔήb=480Θ°Τδ÷–’ΐ»ΖΒΡ «

AΘ°ΔΌΔΎΔέ BΘ°ΔΌΔΎΔή CΘ°ΔΌΔέΔή DΘ°ΔΌΔΎΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΖΫ±ψ –ΟώΆ®––Θ§Ρ≥Ιψ≥ΓΦΤΜ°Ε‘Τ¬Ϋ«ΈΣ30ΓψΘ§Τ¬≥ΛΈΣ60ΟΉΒΡ–±Τ¬ABΫχ––ΗΡ‘λΘ§‘Ύ–±Τ¬÷–ΒψD¥ΠΆΎ»Ξ≤ΩΖ÷Τ¬ΧεΘ®“θ”Α±μ ΨΘ©Θ§–όΫ®“ΜΗωΤΫ––”ΎΥ°ΤΫœΏCAΒΡΤΫΧ®DEΚΆ“ΜΧθ–¬ΒΡ–±Τ¬BEΘ°
Θ®1Θ©»τ–όΫ®ΒΡ–±Τ¬BEΒΡΤ¬Ϋ«ΈΣ36ΓψΘ§‘ρΤΫΧ®DEΒΡ≥Λ‘ΦΈΣΕύ…ΌΟΉΘΩ
Θ®2Θ©‘ΎΨύάκΤ¬Ϋ«AΒψ27ΟΉ‘ΕΒΡG¥Π «…Χ≥Γ÷ς¬ΞΘ§–ΓΟς‘ΎDΒψ≤βΒΟ÷ς¬ΞΕΞ≤ΩH ΒΡ―ωΫ«ΈΣ30ΓψΘ§Ρ«Ο¥÷ς¬ΞGHΗΏ‘ΦΈΣΕύ…ΌΟΉΘΩΘ®ΫαΙϊ»Γ’ϊ ΐΘ§≤ΈΩΦ ΐΨίΘΚsin36Γψ=0.6Θ§cos36Γψ=0.8Θ§tan36Γψ=0.7Θ§ ![]() =1.7Θ©
=1.7Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
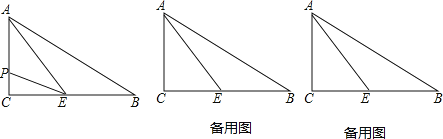
Θ§![]() Θ§ΒψE «BCΒΡ÷–ΒψΘ§Ε·ΒψP¥”AΒψ≥ωΖΔΘ§“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ί
Θ§ΒψE «BCΒΡ÷–ΒψΘ§Ε·ΒψP¥”AΒψ≥ωΖΔΘ§“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ί![]() ‘ΥΕ·Θ°»τ…ηΒψP‘ΥΕ·ΒΡ ±Φδ «tΟκȧѫϥ±t»ΓΚΈ÷Β ±Θ§
‘ΥΕ·Θ°»τ…ηΒψP‘ΥΕ·ΒΡ ±Φδ «tΟκȧѫϥ±t»ΓΚΈ÷Β ±Θ§![]() ΒΡΟφΜΐΒ»”Ύ10ΘΩ
ΒΡΟφΜΐΒ»”Ύ10ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com