
����Ŀ��Ϊ��������ͨ�У�ij�㳡�ƻ����½�Ϊ30�㣬�³�Ϊ60��б��AB���и��죬��б���е�D����ȥ�������壨��Ӱ��ʾ������һ��ƽ����ˮƽ��CA��ƽ̨DE��һ���µ�б��BE��
��1��������б��BE���½�Ϊ36�㣬��ƽ̨DE�ij�ԼΪ�����ף�
��2���ھ����½�A��27��Զ��G�����̳���¥��С����D������¥����H ������Ϊ30�㣬��ô��¥GH��ԼΪ�����ף������ȡ�������ο����ݣ�sin36��=0.6��cos36��=0.8��tan36��=0.7�� ![]() =1.7��
=1.7��
���𰸡�
��1���⣺������б��BE���½ǣ�����BEF��Ϊ36�㣬
���BEF=36�㣬
�ߡ�DAC=��BDF=30�㣬AD=BD=30��
��BF= ![]() BD=15��DF=15
BD=15��DF=15 ![]() ��25.98��
��25.98��
EF= ![]() =
= ![]() ��21.43
��21.43
�ʣ�DE=DF��EF=4���ף���
��2���⣺����D��DP��AC������ΪP�� 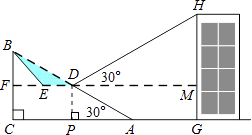
��Rt��DPA��DP= ![]() AD=
AD= ![]() ��30=15��
��30=15��
PA=ADcos30��= ![]() ��30=15
��30=15 ![]() ��
��
�ھ���DPGM�У�MG=DP=15��DM=PG=15 ![]() +27��
+27��
��Rt��DMH��
HM=DMtan30��= ![]() ����15
����15 ![]() +27��=15+9
+27��=15+9 ![]() ��
��
GH=HM+MG=15+15+9 ![]() ��45�ף�
��45�ף�
�𣺽�����GH��ԼΪ45�ף�
����������1����Ϊ����б��BE���½ǣ�����BEF��Ϊ36�㣬�ɡ�DAC=��BDF��AD=BD���õ�BF= ![]() BD��DF��25.98�����ݽ�ֱ��������EF=
BD��DF��25.98�����ݽ�ֱ��������EF= ![]() =
= ![]() ��21.43���õ�DE=DF��EF����2������ʵ������õ�ͼ�Σ���Rt��DPA�У�DP=
��21.43���õ�DE=DF��EF����2������ʵ������õ�ͼ�Σ���Rt��DPA�У�DP= ![]() AD��PA=ADcos30�㣬�ھ���DPGM�У�MG=DP����Rt��DMH�У�HM=DMtan30�㣬�õ�GH=HM+MG.
AD��PA=ADcos30�㣬�ھ���DPGM�У�MG=DP����Rt��DMH�У�HM=DMtan30�㣬�õ�GH=HM+MG.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A��C������ֱ�Ϊ��10��0������0��4������D��OA���е㣬��P��BC���˶�������ODP������Ϊ5�ĵ���������ʱ����P������Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ծ���OABC�Ķ���OΪԭ�㣬OA���ڵ�ֱ��Ϊx�ᣬOC���ڵ�ֱ��Ϊy�ᣬ����ƽ��ֱ������ϵ����֪OA=3��OC=2����E��AB���е㣬��OA��ȡһ��D������BDA��BD���ۣ�ʹ��A����BC���ϵĵ�F����
��1��ֱ��д����E��F�����ꣻ
��2���趥��ΪF�������߽�y���������ڵ�P�����Ե�E��F��PΪ������������ǵ��������Σ���������ߵĽ���ʽ��
��3����x�ᡢy�����Ƿ�ֱ���ڵ�M��N��ʹ���ı���MNFE���ܳ���С��������ڣ�����ܳ�����Сֵ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ֽƬABCD�У�AB��4��BC��6������ABC��AC�۵���ʹ��B���ڵ�E����CE��AD�ڵ�F����DF�ij�����(����)

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�����BD����O��BD���е㣬��M��N�DZ�AD�ϵ����㣬����MO��NO�����ֱ��ӳ�����BC������M�䡢N�䣬��ͼ�е�ȫ�������ι��У� ��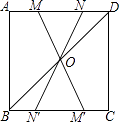
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ϊ�˽�ȫ�����꼶ѧ������ѧ֪ʶ�������������һ����ѧ����У���ȫ��2000���꼶�����������ȡ����ѧ������ѧ�ɼ����е��飬�������������Ƴ�����ͼ����

��1������![]() ��
��![]() ����ʾ�����ֱ�Ϊ��
����ʾ�����ֱ�Ϊ��![]() ��
��![]() ��
��
��2������ͼ�в�ȫƵ���ֲ�ֱ��ͼ��
��3������ѳɼ���100�����ϣ���100�֣���Ϊ���㣬��ô����2000�����꼶������ѧ�ɼ�Ϊ�����ѧ��Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬��D��E�ֱ��DZ�BC��AB�ϵ��е㣬����DE���ӳ�����F��ʹEF=2DF������CE��AF��
��1��֤����AF=CE��
��2������B=30��ʱ�����ж��ı���ACEF����״��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ҫʹƽ���ı���ABCD�������Σ���Ӧ���ӵ�һ��������______(����һ����������)��
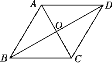
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ε��ܳ�Ϊ20 cm���ױ߳�Ϊx cm��һ����Ϊy cm����y��x֮��ĺ�������ʽ��ȷ����(����)
A. y��20��2x(0��x��20) B. y��20��2x(0��x��10)
C. y��![]() (20��x)(0��x��20) D. y��
(20��x)(0��x��20) D. y��![]() (20��x)(0��x��10)
(20��x)(0��x��10)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com