Question

【题目】如图，在正方形ABCD中，连接BD，点O是BD的中点，若M、N是边AD上的两点，连接MO、NO，并分别延长交边BC于两点M′、N′，则图中的全等三角形共有（ ）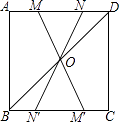

A.2对
B.3对
C.4对
D.5对

Answer 1

【答案】C
【解析】解：∵四边形ABCD是正方形，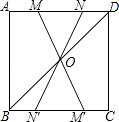

∴AB=CD=CB=AD，∠A=∠C=∠ABC=∠ADC=90°，AD∥BC，

在△ABD和△BCD中，

，

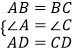∴△ABD≌△BCD，

∵AD∥BC，

∴∠MDO=∠M′BO，

在△MOD和△M′OB中，

，

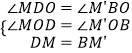∴△MDO≌△M′BO，同理可证△NOD≌△N′OB，∴△MON≌△M′ON′，

∴全等三角形一共有4对．

故答案为：C．

根据正方形的性质，四条边相等，四个角相等，对边平行，由四边形ABCD是正方形，得到△ABD≌△BCD（SAS）、△MDO≌△M′BO（AAS），△NOD≌△N′OB，△MON≌△M′ON′，所以全等三角形一共有4对．