
����Ŀ������ѧ���о����֣�һ������£�һ�ڿ�40�����У�ѧ����ע�������ʦ���εı仯���仯����ʼ�Ͽ�ʱ��ѧ����ע��������ǿ���м���һ��ʱ��ѧ����ע�������ֽ�Ϊ������ȶ�״̬�����ѧ����ע������ʼ��ɢ������ʵ�������֪��ѧ����ע����ָ����y��ʱ��x�����ӣ��ı仯��������ͼ��ʾ������AB��BC�ֱ�Ϊ�߶Σ�CDΪ˫���ߵ�һ���֣���
��1����ʼ�Ͽκ�������ʱ�����ʮ����ʱ��Ƚϣ���ʱѧ����ע���������У�
��2��һ����ѧ�����⣬��Ҫ��19���ӣ�Ϊ��Ч���Ϻã�Ҫ��ѧ����ע����ָ������ʹﵽ36����ô�����ʵ����ţ���ʦ�ܷ���ѧ��ע�����ﵽ�����״̬�½����������Ŀ��
���𰸡�
��1���⣺���߶�AB���ڵ�ֱ�ߵĽ���ʽΪy1=k1x+20��
��B��10��40������ã�k1=2��
��y1=2x+20��
��C��D����˫���ߵĽ���ʽΪy2= ![]() ��
��
��C��25��40������ã�k2=1000��
�� ![]()
��x1=5ʱ��y1=2��5+20=30��
�� ![]() ��
��
��y1��y2
���30����ע���������У�
��2���⣺��y1=36��
��36=2x+20��
��x1=8
��y2=36��
�� ![]() ��
��
�� ![]()
��27.8��8=19.8��19��
�ྭ���ʵ����ţ���ʦ����ѧ��ע�����ﵽ�����״̬�½����������Ŀ��
����������1������һ�κ����ͷ�����������Ӧ�ã��ô���ϵ��������߶�AB���ڵ�ֱ�ߵĽ���ʽ����C��D����˫���ߵĽ���ʽ����x1=5ʱ�� ![]() ���бȽϵõ�y1��y2���ó���30����ע���������У���2����y1=36ʱ���õ�x1=8����y2=36���õ�
���бȽϵõ�y1��y2���ó���30����ע���������У���2����y1=36ʱ���õ�x1=8����y2=36���õ� ![]() ����27.8��8=19.8��19�����Ծ����ʵ����ţ���ʦ����ѧ��ע�����ﵽ�����״̬�½����������Ŀ.
����27.8��8=19.8��19�����Ծ����ʵ����ţ���ʦ����ѧ��ע�����ﵽ�����״̬�½����������Ŀ.


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�����BD����O��BD���е㣬��M��N�DZ�AD�ϵ����㣬����MO��NO�����ֱ��ӳ�����BC������M�䡢N�䣬��ͼ�е�ȫ�������ι��У� ��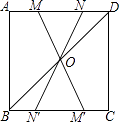
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c����|a��![]() |+
|+![]() +��c��4
+��c��4![]() ��2=0��
��2=0��
��1����a��b��c��ֵ��
��2���ж���a��b��cΪ���ܷ������Σ����ܹ��������Σ�����������ʲô��״������������ε�����������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһ����ϵ�У�һ�κ���y=��mx+n2����κ���y=x2+m��ͼ������ǣ� ��
A.
B.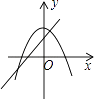
C.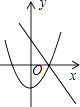
D.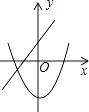
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������Ϸ��һ�������Ĵ�����װ����ͬ��С��3�������Ϸֱ��������1��2��3�����ȣ��״����������һ����Ȼ���Ҵ�ʣ�µ������������һ���Ƚ����ϵ����֣��ϴ�Ļ�ʤ��
��1�����������������3����ĸ��ʣ�
��2�������Ϸ��ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ε��ܳ�Ϊ20 cm���ױ߳�Ϊx cm��һ����Ϊy cm����y��x֮��ĺ�������ʽ��ȷ����(����)
A. y��20��2x(0��x��20) B. y��20��2x(0��x��10)
C. y��![]() (20��x)(0��x��20) D. y��
(20��x)(0��x��20) D. y��![]() (20��x)(0��x��10)
(20��x)(0��x��10)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��BC��AEƽ�֡�BAD��BC�ڵ�E��AE��DE����1+��2=90����M��N�ֱ���BA��CD�ӳ����ϵĵ㣬��EAM�͡�EDN��ƽ���߽��ڵ�F�����н��ۣ���AB��CD���ڡ�AEB+��ADC=180������DEƽ�֡�ADC���ܡ�FΪ��ֵ�����н�����ȷ���У� ��

A. 4��B. 1��C. 2��D. 3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ִ���18����/ʱ���ٶ����������У�����A����õ���P�����ı�ƫ��60��ķ����ϣ���������ʻ20���Ӻ���B���ֲ�õ���P�����ı�ƫ��45�㷽���ϣ����ִ����������̾��룮����ȷ��0.1�� ![]() ��1.73��
��1.73��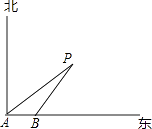
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ�����ڡ�ABC�У�AB��BC��AC���ߵij��ֱ�Ϊ![]() ��
��![]() ��
��![]() ����������ε������С��ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ����ʾ�������������ABC�ĸߣ�������������ܼ�������������
����������ε������С��ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ����ʾ�������������ABC�ĸߣ�������������ܼ�������������
��1�����㽫��ABC�����ֱ����д�ں����ϣ��� ����
˼ά��չ��
��2�����ǰ��������ABC����ķ���������ͼ���������ABC���ߵij��ֱ�![]() a��
a��![]() a��
a��![]() a��a��0����������ͼ�ڵ�����������ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC����������������
a��a��0����������ͼ�ڵ�����������ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC����������������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com