
【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
(1)求证:OB=OC;
(2)若∠ABC=55°,求∠BOC的度数.

【答案】(1)证明见解析;(2)∠BOC=110°.
【解析】试题分析:(1)根据等腰三角形的性质可得:∠ABC=∠ACB,由同角的余角相等可得:∠ABD=∠ACE,进而推出∠OBC=∠OCB解答即可;
(2)容易得而出∠ABC=∠ACB=55°,进而推出∠A=70°,再根据∠BOC=∠EOD=360°-∠A-∠ADB-∠AEC解答即可.
试题解析:(1)证明:∵AB=AC ,∴∠ABC=∠ACB,
∵BD、CE是△ABC的两条高线,
∴∠BEC=∠BDC=90°.∴△BEC≌△CDB.∴∠DBC=∠ECB,BE=CD.
在△BOE和△COD中,
∵∠BOE=∠COD,BE=CD,∠BEC=∠BDE=90°.
∴△BOE≌△COD,∴OB=OC;
(2)∵∠ABC=55°,AB=AC,∴∠A=180°﹣2×55°=70°,
∴∠DOE+∠A=180°.∴∠BOC=∠DOE=180°﹣70°=110°.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】面试时,某人的基本知识、表达能力、工作态度的成绩分别是90分、80分、85分,若依次按20%、40%、40%的比例确定成绩,则这个人的面试成绩是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种品牌运动服经过两次降价,每件零售价由480元降为270元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是
A. 480(1+x)2=270 B. 480(1-x)2=270
C. 480(1-2x)2=270 D. 480(1-x2)=270
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE.
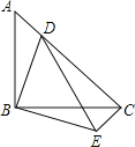
(1)求∠DCE的度数;
(2)当AB=8,AD∶DC=1∶3时,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com