
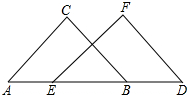
 如图,AC∥EF,AC=EF,AE=BD,△ABC与△EDF全等吗?BC∥DF吗?请说明理由.
如图,AC∥EF,AC=EF,AE=BD,△ABC与△EDF全等吗?BC∥DF吗?请说明理由.
|


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
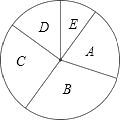 2011年,在长沙创建全国文明城市过程中,某学校数学兴趣小组对全校1500名学生中的部分学生进行了“垃圾分类知识”的抽样测试调查,测试问卷采用等级计分.该兴趣小组把收集到的数据统计成以下表格.
2011年,在长沙创建全国文明城市过程中,某学校数学兴趣小组对全校1500名学生中的部分学生进行了“垃圾分类知识”的抽样测试调查,测试问卷采用等级计分.该兴趣小组把收集到的数据统计成以下表格.| 等级 | A | B | C | D | E |
| 频数 | 40 | 60 | m | 30 | 20 |
| 频率 | 0.2 | n | 0.25 | 0.15 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
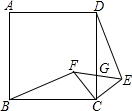 如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
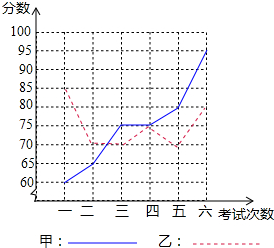 甲、乙两名同学进入初四后,某科6次考试成绩如图:
甲、乙两名同学进入初四后,某科6次考试成绩如图:| 平均数 | 方差 | 中位数 | 众数 | 极差 | |
| 甲 | 75 | 75 | |||
| 乙 | 33.3 | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com