
分析 先根据分式的混合运算顺序和法则化简原式,再代入求值即可得.
解答 解:原式=$\frac{(b-a)(b+a)}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{(b+a)(b-a)}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{b+a}{b-a}$,
当a=$\sqrt{3}+1$,b=$\sqrt{3}-1$时,
原式=$\frac{\sqrt{3}+1+\sqrt{3}-1}{\sqrt{3}-1-\sqrt{3}-1}$=$\frac{2\sqrt{3}}{-2}$=-$\sqrt{3}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和法则是解题的关键.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:填空题
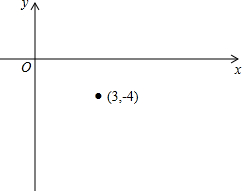 已知反比例函数y=$\frac{k}{x}$的图象经过点(-3,4).
已知反比例函数y=$\frac{k}{x}$的图象经过点(-3,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
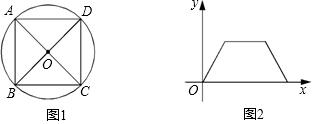
| A. | 线段OA→劣弧AD→线段DO | B. | 劣弧AD→线段DO→线段OC | ||
| C. | 劣弧AD→劣弧DC→线段CO | D. | 线段OB→劣弧BC→劣弧CD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
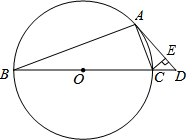 如图,⊙O是△ABC的外接圆,BC为⊙O的直径,作∠CAD=∠B,且点E在BC的延长线上,CE⊥AD于点E,
如图,⊙O是△ABC的外接圆,BC为⊙O的直径,作∠CAD=∠B,且点E在BC的延长线上,CE⊥AD于点E,查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com