
 如图,小刚从点A出发,沿着坡度为α的斜坡向上走了650米到达点B,且
如图,小刚从点A出发,沿着坡度为α的斜坡向上走了650米到达点B,且分析 (1)根据题意画出图形,进而利用锐角三角函数关系分别求出BF;
(2)利用坡度的定义求得CE的长,即可得出点C相对于起点A升高的高度.
解答 解:(1)如图所示:过点B作BF⊥AD于点F,过点C作CD⊥AD于点D,
由题意得:AB=650米,BC=1千米,
∴sinα=$\frac{5}{13}$=$\frac{BF}{AB}$=$\frac{BF}{650}$,
∴BF=650×$\frac{5}{13}$=250(米),
∴小明从A点到点B上升的高度是250米;
(2)∵斜坡BC的坡度为:1:3,
∴CE:BE=1:3,
设CE=x,则BE=3x,
由勾股定理得:x2+(3x)2=10002,
解得:x=100$\sqrt{10}$,
∴CD=CE+DE=BF+CE=250+100$\sqrt{10}$,
答:点C相对于起点A升高了(250+100$\sqrt{10}$)米.
故答案为:250.
点评 此题主要考查了解直角三角形的应用,根据题意构造直角三角形,正确选择锐角三角函数得出BF,CE的长是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 题目 | 在山脚下测量铁塔顶端到山底的高度 | |
| 测量 目标 图示 |  | 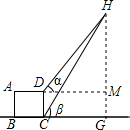 |
| CD=5m | ∠α=45°,∠β=47° | |
| A. | 64.87m | B. | 74.07m | C. | 84.08m | D. | 88.78m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图棋盘上有黑、白两色棋子若干,找出所有三颗颜色相同的棋并且在同一直线上的直线,这样直线共有多少条( )
如图棋盘上有黑、白两色棋子若干,找出所有三颗颜色相同的棋并且在同一直线上的直线,这样直线共有多少条( )| A. | 6条 | B. | 5条 | C. | 4条 | D. | 3条 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com