
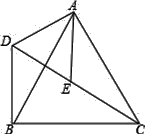
【题目】如图,△ACB和△ADE均为等边三角形,点C、E、D在同一直线上,在△ACD中,线段AE是CD边上的中线,连接BD.求证:CD=2BD.
 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
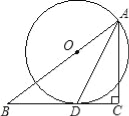
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以O为圆心,OA为半径的⊙O经过点D.
(1)求证:BC是⊙O的切线;
(2)若BD=5,DC=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应我市创建“全国卫生城市”的号召,某校1500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等,从中随机抽取了部分学生成绩进行统计,绘制成如图两幅不完整的统计图表,根据图表信息,以下说法不正确的是( ) 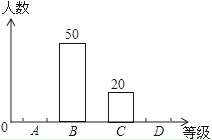
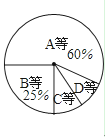
A.D等所在扇形的圆心角为15°
B.样本容量是200
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年的“六一”儿童节是个星期五,某校学生会在初一年级进行了学生对学校作息安排的三种期望(全天休息、半天休息、全天上课)的抽样调查,并把调查结果绘成了下面两个统计图,已知此次被调查的男、女学生人数相同.根据图中信息,下列判断:①在被调查的学生中,期望全天休息的人数占53%;②本次调查了200名学生;③在被调查的学生中,有30%的女生期望休息半天;④若该校现有初一学生900人,根据调查结果估计期望至少休息半天的学生超过了720人.其中正确的判断有( ) 

A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH是什么四边形?证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? . (填一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题:①若a>b,则a+1>b+1;②若a>b,则a﹣1>b﹣1;③若a>b,则﹣2a<﹣2b;④若a>b,则ac>bc.其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AD⊥BC于D,CE⊥AB于E.
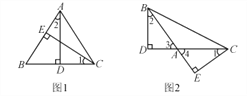
(1)猜测∠1与∠2的关系,并说明理由;
如果∠BAC是钝角,如图2,(1)中的结论是否还成立?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com