
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH是什么四边形?证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? . (填一种即可)
【答案】(1)四边形EFGH的形状是平行四边形.理由见解析;(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.(3)矩形.
【解析】
试题解析:(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=![]() BD,FG∥BD,FG=
BD,FG∥BD,FG=![]() BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
(3)菱形的中点四边形是矩形.根据三角形的中位线平行于第三边并且等于第三边的一半可得EH∥BD,EF∥AC,再根据矩形的每一个角都是直角可得∠1=90°,然后根据平行线的性质求出∠3=90°,再根据垂直定义解答.
试题解析:(1)四边形EFGH的形状是平行四边形.理由如下:
如图,连结BD.
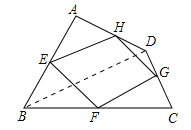
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=![]() BD,
BD,
同理FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
如图,连结AC、BD.
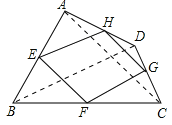
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
(3)菱形的中点四边形是矩形.理由如下:
如图,连结AC、BD.
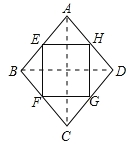
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,FG∥BD,EH=![]() BD,FG=
BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EH∥BD,HG∥AC,
∴EH⊥HG,
∴平行四边形EFGH是矩形.


科目:初中数学 来源: 题型:
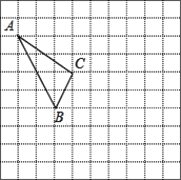
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为A(-4,5),C(-1,3).
(1)请在如图所示的网格内作出x轴、y轴;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标并求出△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计分析,绘制了如下不完整的统计表和统计图. 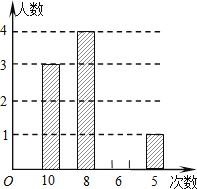
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a=;
(2)请将条形统计图补充完整;
查看答案和解析>>
科目:初中数学 来源: 题型:
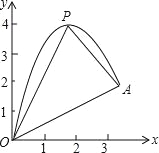
【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com