
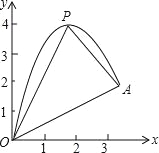
【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
【答案】(1)最高点P的坐标为(2,4);(2)点A的坐标为(![]() ,
,![]() );(3)
);(3)![]() ;(4)点M的坐标为(
;(4)点M的坐标为(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用配方法抛物线的一般式化为顶点式,即可求出二次函数图象的最高点P的坐标;
(2)联立两解析式,可求出交点A的坐标;
(3)作PQ⊥x轴于点Q,AB⊥x轴于点B.根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA,代入数值计算即可求解;
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,由于两平行线之间的距离相等,根据同底等高的两个三角形面积相等,可得△MOA的面积等于△POA的面积.设直线PM的解析式为y=![]() x+b,将P(2,4)代入,求出直线PM的解析式为y=
x+b,将P(2,4)代入,求出直线PM的解析式为y=![]() x+3.再与抛物线的解析式联立,得到方程组
x+3.再与抛物线的解析式联立,得到方程组 ,解方程组即可求出点M的坐标.
,解方程组即可求出点M的坐标.
试题解析:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,
故二次函数图象的最高点P的坐标为(2,4);
(2)联立两解析式可得: ,解得:
,解得:![]() ,或
,或![]() .
.
故可得点A的坐标为(![]() ,
,![]() );
);
(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.

S△POA=S△POQ+S△梯形PQBA﹣S△BOA
=![]() ×2×4+
×2×4+![]() ×(
×(![]() +4)×(
+4)×(![]() ﹣2)﹣
﹣2)﹣![]() ×
×![]() ×
×![]()
=4+![]() ﹣
﹣![]()
=![]() ;
;
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.
设直线PM的解析式为y=![]() x+b,
x+b,
∵P的坐标为(2,4),
∴4=![]() ×2+b,解得b=3,
×2+b,解得b=3,
∴直线PM的解析式为y=![]() x+3.
x+3.
由 ,解得
,解得![]() ,
, ,
,
∴点M的坐标为(![]() ,
,![]() ).
).



科目:初中数学 来源: 题型:
【题目】如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a , 宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( ) 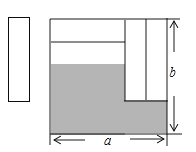
A.a+2b
B.4a
C.4b
D.2a+b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年的“六一”儿童节是个星期五,某校学生会在初一年级进行了学生对学校作息安排的三种期望(全天休息、半天休息、全天上课)的抽样调查,并把调查结果绘成了下面两个统计图,已知此次被调查的男、女学生人数相同.根据图中信息,下列判断:①在被调查的学生中,期望全天休息的人数占53%;②本次调查了200名学生;③在被调查的学生中,有30%的女生期望休息半天;④若该校现有初一学生900人,根据调查结果估计期望至少休息半天的学生超过了720人.其中正确的判断有( ) 

A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH是什么四边形?证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? . (填一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题:①若a>b,则a+1>b+1;②若a>b,则a﹣1>b﹣1;③若a>b,则﹣2a<﹣2b;④若a>b,则ac>bc.其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某调查机构将今年温州市民最关注的热点话题分为消费、教育、环保、反腐及其它共五类.根据最近一次随机调查的相关数据,绘制的统计图表如下:
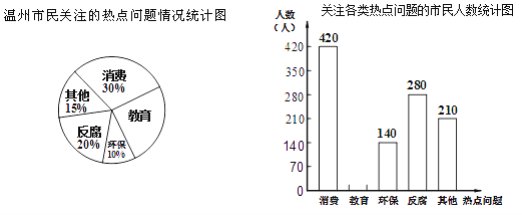
根据以上信息解答下列问题:
(1)本次共调查人________,请在补全条形统计图并标出相应数据________;
(2)若温州市约有900万人口,请你估计最关注教育问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,求抽取的两人恰好是甲和乙的概率(列树状图或列表说明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若AB=BC,则点B为线段AC的中点 B. 射线AB和射线BA是同一条射线
C. 两点之间的线段就是两点之间的距离 D. 同角的补角一定相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com