
【题目】如图,直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=AC,过点B作BE⊥AC于点E. 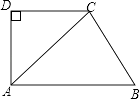
(1)求证:△ADC≌△BEA;
(2)若AD=4,CD=3,求BC的长.
【答案】
(1)证明:∵BE⊥AC,
∴∠1=90°,
∵AB∥CD,
∴∠2=∠3,
在△ADC和△BEA中,
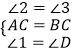 ,
,
∴△ADC≌△BEA(ASA);

(2)解:∵△ADC≌△BEA,
∴AD=BE=4,AE=CD=3,
在Rt△ADC中:AC= ![]() =5,
=5,
∴CE=5﹣3=2,
在Rt△CEB中:BC= ![]() =
= ![]() =2
=2 ![]() .
.
【解析】(1)首先根据垂直可得∠1=∠D=90°,再根据AB∥CD可得∠2=∠3,然后再有条件AC=BC可利用ASA证明△ADC≌△BEA;(2)首先根据全等三角形的性质可得AD=BE=4,AE=CD=3,在Rt△ADC中利用勾股定理可得AC=5,然后再在Rt△CEB中利用勾股定理计算出BC长即可.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,将一副直角三角板放在同一条直线AB上,其中![]() ,
,![]() .
.
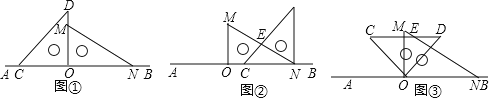
![]() 将图1中的三角尺OCD沿AB的方向平移至图
将图1中的三角尺OCD沿AB的方向平移至图![]() 的位置,使得点O与点N重合,CD与MN相交于点E,求
的位置,使得点O与点N重合,CD与MN相交于点E,求![]() 的度数;
的度数;
![]() 将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在
将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在![]() 的内部,如图3,且OD恰好平分
的内部,如图3,且OD恰好平分![]() ,CD与MN相交于点E,求
,CD与MN相交于点E,求![]() 的度数;
的度数;
![]() 将图1中的三角尺OCD绕点O按每秒
将图1中的三角尺OCD绕点O按每秒![]() 的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直
的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直![]() 直接写出结果
直接写出结果![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
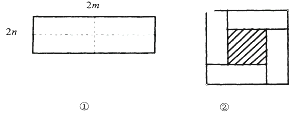
(1)你认为图②中的阴影部分的正方形的边长等于_________________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①_________________________________________________________.
方法②_________________________________________________________.
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式间的等量关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自行车队进行训练,训练时所有队员都以相同的速度前进,突然,1号队员以每小时比其他队员快10千米的速度独自行进,行进了10千米后掉转车头,速度不变往回骑,直到与其他的队员会合.从1号队员离队开始到与其他队员重新会合,经过了15分钟.
(1)其他队员的行进速度是多少?
(2)1号队员从离队开始到与队员重新会合这个过程中,经过多长时间与其他队员相距1千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示. 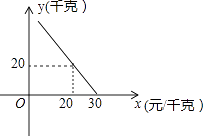
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是某网络书店![]() 月关于图书销售情况的两个统计图:
月关于图书销售情况的两个统计图:

(![]() )求
)求![]() 月份该网络书店绘本类图书的销售额.
月份该网络书店绘本类图书的销售额.
(![]() )若已知
)若已知![]() 月份与
月份与![]() 月份这两个月的绘本类图书销售额相同,请补全统计图
月份这两个月的绘本类图书销售额相同,请补全统计图![]() .
.
(![]() )有以下两个结论:
)有以下两个结论:
①该书店第一季度的销售总额为![]() 万元.
万元.
②该书店![]() 月份到
月份到![]() 月份绘本类图书销售额的月增长率相等.
月份绘本类图书销售额的月增长率相等.
请你判断以上两个结论是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )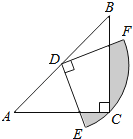
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论中一定成立的个数是( )
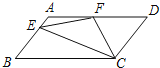
①∠DCF=![]() ∠BCD;②EF=CF;③
∠BCD;②EF=CF;③![]() ;④∠DFE=3∠AEF.
;④∠DFE=3∠AEF.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com