
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )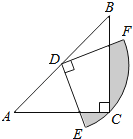
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
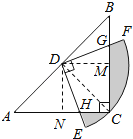
【解析】解:连接CD,作DM⊥BC,DN⊥AC.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴DC=![]() AB=1,四边形DMCN是正方形,DM=
AB=1,四边形DMCN是正方形,DM=![]() .
.
则扇形FDE的面积是:![]() =
=![]() .
.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴CD平分∠BCA,
又∵DM⊥BC,DN⊥AC,
∴DM=DN,
∵∠GDH=∠MDN=90°,
∴∠GDM=∠HDN,
则在△DMG和△DNH中,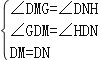 ,
,
∴△DMG≌△DNH(AAS),
∴S四边形DGCH=S四边形DMCN=![]() .
.
则阴影部分的面积是:![]() ﹣
﹣![]() .
. 
【考点精析】掌握扇形面积计算公式是解答本题的根本,需要知道在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
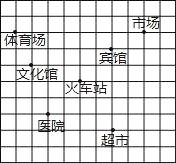
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系.
(2)写出市场的坐标为 ;超市的坐标为 .
(3)请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,画出平移后的△A1B1C1,并求出其面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知开口向下的抛物线y1=ax2﹣2ax+1过点A(m,1),与y轴交于点C,顶点为B,将抛物线y1绕点C旋转180°后得到抛物线y2 , 点A,B的对应点分别为点D,E.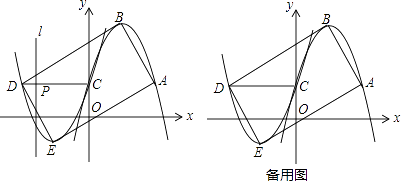
(1)直接写出点A,C,D的坐标;
(2)当四边形ABCD是矩形时,求a的值及抛物线y2的解析式;
(3)在(2)的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点C停止,在点P运动的过程中,过点P作直线l⊥x轴,将矩形ABDE沿直线l折叠,设矩形折叠后相互重合部分面积为S平方单位,点P的运动时间为t秒,求S与t的函数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=AC,过点B作BE⊥AC于点E. 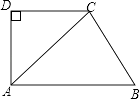
(1)求证:△ADC≌△BEA;
(2)若AD=4,CD=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过对某校营养午餐的检测,得到如下信息:每份营养午餐的总质量![]() ;午餐的成分
;午餐的成分
为蛋白质、碳水化合物、脂肪和矿物质,其组成成分所占比例如图![]() 所示;其中矿物质的含量是脂
所示;其中矿物质的含量是脂
肪含量的![]() 倍,蛋白质和碳水化合物含量占
倍,蛋白质和碳水化合物含量占![]() .
.

(![]() )设其中蛋白质含量是
)设其中蛋白质含量是![]() .脂肪含量是
.脂肪含量是![]() ,请用含
,请用含![]() 或
或![]() 的代数式分别表示碳水化合物和矿物
的代数式分别表示碳水化合物和矿物
质的质量.
(![]() )求每份营养午餐中蛋白质、碳水化合物、脂肪和矿物质的质量.
)求每份营养午餐中蛋白质、碳水化合物、脂肪和矿物质的质量.
(![]() )参考图
)参考图![]() ,请在图
,请在图![]() 中完成这四种不同成分所占百分比的扇形统计图.
中完成这四种不同成分所占百分比的扇形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
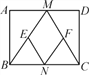
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)当AB∶AD=___时,四边形MENF是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件不能用来判定四边形ABCD是平行四边形的是( )
A. ∠A:∠B:∠C:∠D=1:4:1:4 B. AB∥CD,AD=BC
C. AB=CD,AD=BC D. AB∥CD,AD∥CB
查看答案和解析>>
科目:初中数学 来源: 题型:
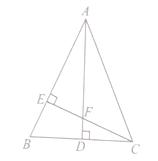
【题目】如图,在△ABC中,AB=AC, AD是∠BAC的平分线,AD⊥BC, CE⊥AB.CE交AD于点F,AE=CE.
(1)你能说明△AEF与△CEB全等吗?
(2)若AF=12cm,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小,质地都相同的乒乓球,球面上分别标有数字1,-2,3,-4,小明先从布袋中随机摸出一个球(不放回去),再从剩下的3个球中随机摸出第二个乒乓球.
(1)共有几种可能的结果?
(2)请用画树状图或列表的方法求两次摸出的乒乓球的数字之积为偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com