
【题目】如图,在△ABC中,AB=AC, AD是∠BAC的平分线,AD⊥BC, CE⊥AB.CE交AD于点F,AE=CE.
(1)你能说明△AEF与△CEB全等吗?
(2)若AF=12cm,求CD的长.
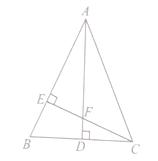
【答案】(1)证明见解析(2)6cm
【解析】(1)根据直角三角形两锐角互余可推得∠EAF =∠ECB,再结合AE =CE,∠AEF =∠CEB =90°,根据ASA即可得到△AEF≌△CEB;
(2)由△AEF≌△CEB可得BC=AF,再根据等腰三角形的“三线合一”的性质即可求得CD长.
(1)因为AD⊥BC,
所以∠B +∠BAD =90°.
因为CE⊥AB,
所以∠B +∠BCE =90°,
所以∠EAF =∠ECB,
在△AEF和△CEB中,
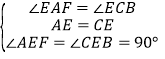 ,
,
所以△AEF≌△CEB(ASA);
(2)因为△AEF ≌△CEB,
所以AF =BC,
因为AB =AC,AD⊥BC,
所以CD =BD =![]() BC,
BC,
所以CD=![]() ×12=6cm.
×12=6cm.


科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
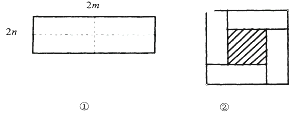
(1)你认为图②中的阴影部分的正方形的边长等于_________________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①_________________________________________________________.
方法②_________________________________________________________.
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式间的等量关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )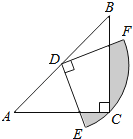
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论中一定成立的个数是( )
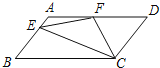
①∠DCF=![]() ∠BCD;②EF=CF;③
∠BCD;②EF=CF;③![]() ;④∠DFE=3∠AEF.
;④∠DFE=3∠AEF.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
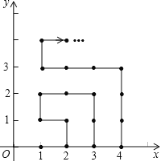
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(2,2)……根据这个规律,第25个点的坐标为____________,第2018个点的坐标为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
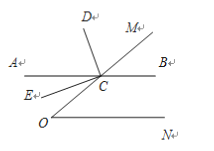
【题目】已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算: ![]()
【答案】![]()
【解析】根据实数的运算顺序,利用二次根式性质,零指数幂法则,首先计算乘方、开方,然后从左向右依次计算.
解:原式=![]() .
.
“点睛”此题主要考查了实数的运算,在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
【题型】解答题
【结束】
22
【题目】已知4x2+y2 -4x-6y+10=0,求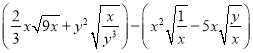 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com