
【题目】某商业集团新建一小车停车场,经测算,此停车场每天需固定支出的费用(设施维修费、车辆管理人员工资等)为800元.为制定合理的收费标准,该集团对一段时间每天小车停放辆次与每辆次小车的收费情况进行了调查,发现每辆次小车的停车费不超过5元时,每天来此处停放的小车可达1440辆次;若停车费超过5元,则每超过1元,每天来此处停放的小车就减少120辆次.为便于结算,规定每辆次小车的停车费x(元)只取整数,用y(元)表示此停车场的日净收入,且要求日净收入不低于2512元.(日净收入=每天共收取的停车费﹣每天的固定支出)
(1)当x≤5时,写出y与x之间的关系式,并说明每辆小车的停车费最少不低于多少元;
(2)当x>5时,写出y与x之间的函数关系式(不必写出x的取值范围);
(3)该集团要求此停车场既要吸引客户,使每天小车停放的辆次较多,又要有较大的日净收入.按此要求,每辆次小车的停车费应定为多少元?此时日净收入是多少?
【答案】(1)y=1440x﹣800;每辆次小车的停车费最少不低于3元;(2)y=﹣120x2+2040x﹣800;(3)每辆次小车的停车费应定为8元,此时的日净收入为7840元.
【解析】
(1)根据题意和公式:日净收入=每天共收取的停车费﹣每天的固定支出,即可求出y与x的关系式,然后根据日净收入不低于2512元,列出不等式,即可求出x的最小整数值;
(2)根据题意和公式:日净收入=每天共收取的停车费﹣每天的固定支出,即可求出y与x的关系式;
(3)根据x的取值范围,分类讨论:当x≤5时,根据一次函数的增减性,即可求出此时y的最大值;当x>5时,将二次函数一般式化为顶点式,即可求出此时y的最大值,从而得出结论.
解:(1)由题意得:y=1440x﹣800
∵1440x﹣800≥2512,
∴x≥2.3
∵x取整数,
∴x最小取3,即每辆次小车的停车费最少不低于3元.
答:每辆小车的停车费最少不低于3元;
(2)由题意得:
y=[1440﹣120(x﹣5)]x﹣800
即y=﹣120x2+2040x﹣800
(3)当x≤5时,
∵1440>0,
∴y随x的增大而增大
∴当x=5时,最大日净收入y=1440×5﹣800=6400(元)
当x>5时,
y=﹣120x2+2040x﹣800
=﹣120(x2﹣17x)﹣800
=﹣120(x﹣![]() )2+7870
)2+7870
∴当x=![]() 时,y有最大值.但x只能取整数,
时,y有最大值.但x只能取整数,
∴x取8或9.
显然,x取8时,小车停放辆次较多,此时最大日净收入为y=﹣120×![]() +7870=7840(元)
+7870=7840(元)
∵7840元>6400元
∴每辆次小车的停车费应定为8元,此时的日净收入为7840元.
答:每辆次小车的停车费应定为8元,此时的日净收入为7840元.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0,
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根?
(2)当Rt△ABC的斜边a=![]() ,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一矩形纸片OABC放在直角坐标系中,O为原点C在x轴上,OA=5,OC=13,如图所示,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,则E点坐标为_____.
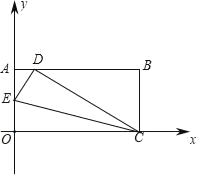
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B,
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=![]() ,求⊙O 的半径.
,求⊙O 的半径.
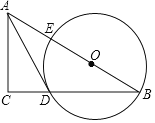
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是 ,点Bn的坐标是 .
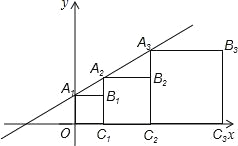
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为住宅区内的两幢楼,它们的高AB=CD=30m,两楼之间的距离AC=24m,现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高?(精确到0.1m,![]() ≈1.41,
≈1.41,![]() ≈1.73)?
≈1.73)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解九年级学生数学模拟考试成绩情况,随机抽取部分学生的成绩进行分析,制成频数分布表如下(成绩得分均为整数):
组别 | 成绩分组 | 频数 | 频率 |
1 | 47.5~59.5 | 2 | 0.05 |
2 | 59.5~71.5 | 4 | 0.10 |
3 | 71.5~83.5 | a | 0.2 |
4 | 83.5~95.5 | 10 | 0.25 |
5 | 95.5~107.5 | b | c |
6 | 107.5~120 | 6 | 0.15 |
合计 | d | 1.00 |
根据表中提供的信息解答下列问题:
(1)频数分布表中的a= ,b= ,c= ,d= ;
(2)补充完整频数分布直方图.
(3)已知全市九年级共有3500名学生参加考试,成绩96分及以上为优秀,估计全市九年级学生数学模拟考试成绩为优秀的学生人数是多少?
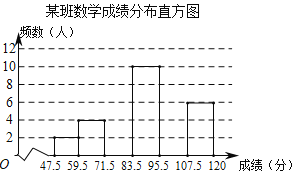
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com