
【题目】如图抛物线y=ax2+bx+c的对称轴是x=﹣1,与x轴的一个交点为(﹣5,0),则不等式ax2+bx+c>0的解集为_____.
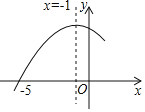
【答案】﹣5<x<3
【解析】
先根据抛物线的对称性得到A点坐标(3,0),由y=ax2+bx+c>0得函数值为正数,即抛物线在x轴上方,然后找出对应的自变量的取值范围即可得到不等式ax2+bx+c>0的解集.
解:根据图示知,抛物线y=ax2+bx+c图象的对称轴是x=﹣1,与x轴的一个交点坐标为(﹣5,0),
根据抛物线的对称性知,抛物线y=ax2+bx+c图象与x轴的两个交点关于直线x=﹣1对称,即
抛物线y=ax2+bx+c图象与x轴的另一个交点与(﹣5,0)关于直线x=﹣1对称,
∴另一个交点的坐标为(3,0),
∵不等式ax2+bx+c>0,即y=ax2+bx+c>0,
∴抛物线y=ax2+bx+c的图形在x轴上方,
∴不等式ax2+bx+c>0的解集是﹣5<x<3.
故答案为﹣5<x<3.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a#0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0;②b2>4ac;③0<b<1;④当x<﹣1时,y<0.其中正确结论的个数是( )
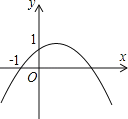
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商业集团新建一小车停车场,经测算,此停车场每天需固定支出的费用(设施维修费、车辆管理人员工资等)为800元.为制定合理的收费标准,该集团对一段时间每天小车停放辆次与每辆次小车的收费情况进行了调查,发现每辆次小车的停车费不超过5元时,每天来此处停放的小车可达1440辆次;若停车费超过5元,则每超过1元,每天来此处停放的小车就减少120辆次.为便于结算,规定每辆次小车的停车费x(元)只取整数,用y(元)表示此停车场的日净收入,且要求日净收入不低于2512元.(日净收入=每天共收取的停车费﹣每天的固定支出)
(1)当x≤5时,写出y与x之间的关系式,并说明每辆小车的停车费最少不低于多少元;
(2)当x>5时,写出y与x之间的函数关系式(不必写出x的取值范围);
(3)该集团要求此停车场既要吸引客户,使每天小车停放的辆次较多,又要有较大的日净收入.按此要求,每辆次小车的停车费应定为多少元?此时日净收入是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足师生的阅读需求,某校图书馆藏书总量由2017年![]() 万册增加到2019年
万册增加到2019年![]() 万册.
万册.
(1)求该校图书馆这两年藏书总量的年均增长率;
(2)经统计知:在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书总量的年均增长率,2019年中外古典名著册数占藏书总量的![]() ,而在2017年中外古典名著册数仅占当年藏书总量的
,而在2017年中外古典名著册数仅占当年藏书总量的![]() ,请求出
,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地盛产樱桃,一年一度的樱桃节期间,很多果园推出了免费品尝和优惠采摘活动,其中甲、乙两家果园的樱桃品质相同,销售价格也相同,但推出了不同的采摘方案:
甲园 | 游客进园需购买 |
乙园 | 游客进园不需购买门票,采摘的樱桃在一定数量以内按原价购买,超过部分打折购买 |
小明和爸爸、妈妈在樱桃节期间也来采摘樱桃,若设他们的樱桃采摘量为![]() (千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为
(千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为![]() (元)在乙采摘园所需总费用为
(元)在乙采摘园所需总费用为![]() (元),图中的折线
(元),图中的折线![]() 表示
表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.

(1)①甲、乙两果园的樱桃单价为_____________元![]() 千克;
千克;
②直接写出![]() 的函数表达式:_________________,并在图中补画出
的函数表达式:_________________,并在图中补画出![]() 的函数图象;
的函数图象;
(2)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若小明一家当天所采摘的樱桃不少于![]() 千克,选择哪个采摘园更划算?请说明理由.
千克,选择哪个采摘园更划算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 .
(2)请用列表法或画树状图法求小明和小亮诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD内有一点P,PA=5,PB=![]() ,PC=
,PC=![]() ,将△BPC绕点B逆时针旋转90°.
,将△BPC绕点B逆时针旋转90°.
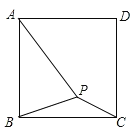
(1)画出旋转后的图形;
(2)求点C和点P′的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
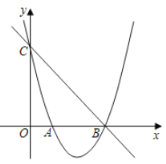
(1)求此抛物线的解析式;
(2)若点![]() 是直线
是直线![]() 下方的抛物线上一动点(不点
下方的抛物线上一动点(不点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
②连接![]() ,
,![]() ,求
,求![]() 的面积最大时点
的面积最大时点![]() 的坐标;
的坐标;
(3)设抛物线的对称轴与![]() 交于点
交于点![]() ,点
,点![]() 是抛物线的对称轴上一点,
是抛物线的对称轴上一点,![]() 为
为![]() 轴上一点,是否存在这样的点
轴上一点,是否存在这样的点![]() 和点
和点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?如果存在,请直接写出点
为顶点的四边形是菱形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,我县某校开展“新学期、新征程,新气象”入学系列教育活动,训练两天后,为了在合唱中给某班学生恰当地分配声部,该校音乐教师李老师随机抽取学生试唱,根据试唱情况把所抽学生分成A、B、C、D四种声部等级,并根据等级统计结果绘制了如图1和如图2两幅不完整的统计图,请根据图中提供的信息完成以下问题:

(1)扇形统计图中D等对应的圆心角的度数是 °,补全条形统计图;
(2)已知A等声部的同学有一位是男生,李老师准备从这4位同学中随机选择两位同学教其他同学,请用列表法或画树状图的方法求出选中的两名同学恰好是一男一女的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com