
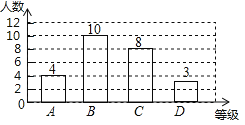
����Ŀ����ѧ��������ijУ��չ����ѧ�ڡ������̣�����������ѧϵ�н������ѵ�������Ϊ���ںϳ��и�ij��ѧ��ǡ���ط�����������У���ֽ�ʦ����ʦ�����ȡѧ���Գ��������Գ����������ѧ���ֳ�A��B��C��D���������ȼ��������ݵȼ�ͳ�ƽ����������ͼ1����ͼ2������������ͳ��ͼ�������ͼ���ṩ����Ϣ����������⣺

��1������ͳ��ͼ��D�ȶ�Ӧ��Բ�ĽǵĶ������� ��������ȫ����ͳ��ͼ��
��2����֪A��������ͬѧ��һλ������������ʦ������4λͬѧ�����ѡ����λͬѧ������ͬѧ�������б�������״ͼ�ķ������ѡ�е�����ͬѧǡ����һ��һŮ�ĸ��ʣ�
���𰸡��������22-1����1��43.2�㣬��ͼ���¼���������2��ѡ�е�����ͬѧǡ����һ��һŮ�ĸ�����![]() ��
��
��������
��1����B�ȼ���������������ռ�İٷֱ�������������ټ�ȥA��B��C�ȼ��������ɵ�D�ȼ����������D�ȼ���ռ�ٷֱȳ���360�ȿɵ�����ͳ��ͼ��D�ȶ�Ӧ��Բ�ĽǵĶ�������2��ѡ����һ��ͬѧ�������Ϊ�У�Ů��Ů��Ů���ڶ���ͬѧ��Ϊʣ���3��������г���״ͼ�����������.
��1��D�ȼ��������У�10��40%��4��10��8��3���ˣ���
������ͳ��ͼ��D�ȶ�Ӧ��Բ�ĽǵĶ�����360���![]() ��43.2�㣬
��43.2�㣬
��ͼ���£�
�ʴ�Ϊ��43.2��
��2������״ͼ���£�
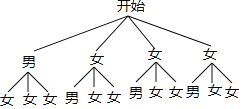
����12�ֵȿ��ܵĽ����������ѡ�е�����ͬѧǡ����һ��һŮ����6�֣�
��ѡ�е�����ͬѧǡ����һ��һŮ�ĸ�����![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������y��ax2+bx+c�ĶԳ�����x����1����x���һ������Ϊ����5��0������ʽax2+bx+c��0�Ľ⼯Ϊ_____��
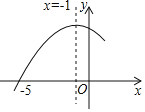
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
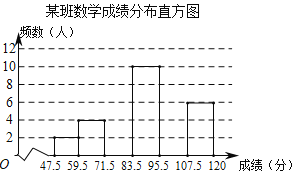
����Ŀ��ij��Ϊ�˽���꼶ѧ����ѧģ�⿼�Գɼ�����������ȡ����ѧ���ijɼ����з������Ƴ�Ƶ���ֲ������£��ɼ��÷־�Ϊ��������
��� | �ɼ����� | Ƶ�� | Ƶ�� |
1 | 47.5��59.5 | 2 | 0.05 |
2 | 59.5��71.5 | 4 | 0.10 |
3 | 71.5��83.5 | a | 0.2 |
4 | 83.5��95.5 | 10 | 0.25 |
5 | 95.5��107.5 | b | c |
6 | 107.5��120 | 6 | 0.15 |
�ϼ� | d | 1.00 |
���ݱ����ṩ����Ϣ����������⣺
��1��Ƶ���ֲ����е�a���� ����b���� ����c���� ����d���� ����
��2����������Ƶ���ֲ�ֱ��ͼ��
��3����֪ȫ�о��꼶����3500��ѧ���μӿ��ԣ��ɼ�96�ּ�����Ϊ���㣬����ȫ�о��꼶ѧ����ѧģ�⿼�Գɼ�Ϊ�����ѧ�������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
��֪ʵ��m��n����(2m3+n3+1)(2m3+n3-1)=80������2m3+n3��ֵ
�⣺��2m3+n3=t����ԭ���̱�Ϊ(t+1)(t-1)=80��������t2-1=80��t2=81�� t=��9������2m3+n3=��9
�������ַ�����Ϊ����Ԫ������������ijЩ���ֿ���һ�����壬��������ĸ����(����Ԫ)������ʹ���ӵ������.
���������Ķ��������ݣ�����������⣬��д��������.
��֪ʵ��x��y����(4x2+4y2+3)(4x2+4y2-3)=27����x2+y2��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����Ϊ40cm����˿�������Σ�����ÿһ����˿�ij���Ϊ�ܳ�����һ��������.
��1��Ҫʹ�����������ε����֮�͵���52cm2����ô�����˿�������κ�ij��ȷֱ��Ƕ��٣�
��2�����������ε����֮�Ϳ��ܵ���48cm2�����ܣ����������˿�ij��ȣ������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���OABC�Ǿ��Σ��ı���ADEF�������Σ���A��D��x��ĸ������ϣ���C��y����������ϣ���F��AB�ϣ���B��E�ڷ���������![]() ��kΪ������k ��0����ͼ���ϣ�������ADEF�����Ϊ16����BF=2AF����kֵΪ
��kΪ������k ��0����ͼ���ϣ�������ADEF�����Ϊ16����BF=2AF����kֵΪ
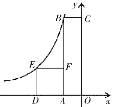
A.��8B.��12C.��24D.��36
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�������Σ���ADF��תһ���ǶȺ�õ���ABE����ͼ��ʾ�����AF=4��AB=7

��1��ָ����ת���ĺ���ת�Ƕ�.
��2����DE�ij���.
��3��BE��DF��ֱ�� ˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��2ax��2��a��0����
��1���ö��κ���ͼ��ĶԳ�����ֱ���� ����
��2�����ö��κ�����ͼ�����ϣ�����1��x��5ʱ������ͼ�����ߵ�ΪM����͵�ΪN����M��������Ϊ![]() �����M�͵�N�����ꣻ
�����M�͵�N�����ꣻ
��3�����ö��κ�����ͼ�����£����ڸö��κ���ͼ���ϵ�����A��x1��y1����B��x2��y2������x2��3ʱ������y1��y2������ͼ��ֱ��д��x1��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������x�Ķ��κ���![]() ��ͼ����x�ύ�ڵ�A(1��0)�͵�B����y�ύ�ڵ�C(0��3)�������ߵĶԳ�����x�ύ�ڵ�D.
��ͼ����x�ύ�ڵ�A(1��0)�͵�B����y�ύ�ڵ�C(0��3)�������ߵĶԳ�����x�ύ�ڵ�D.
(1)����κ����ı���ʽ��
(2)��y�����Ƿ����һ��P��ʹ��PBCΪ����������.�����ڣ��������P�����ꣻ
(3)��һ����M�ӵ�A��������ÿ��1����λ���ٶ���AB�����B�˶�����һ����N�ӵ�D���Mͬʱ��������ÿ��2����λ���ٶ��������ߵĶԳ������˶�������M�� ���Bʱ����M��Nͬʱֹͣ�˶����ʵ�M��N�˶����δ�ʱ����MNB�����������������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com