
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝y£Ωax2©Å2ax©Å2£®a°Ÿ0£©£Æ
£®1£©∏√∂˛¥Œ∫Ø ˝ÕºœÛµƒ∂‘≥∆÷· «÷±œþ°° °°£ª
£®2£©»Ù∏√∂˛¥Œ∫Ø ˝µƒÕºœÛø™ø⁄œÚ…œ£¨µ±©Å1°Ðx°Ð5 ±£¨∫Ø ˝ÕºœÛµƒ◊Ó∏þµ„Œ™M£¨◊ÓµÕµ„Œ™N£¨µ„Mµƒ◊ð◊¯±ÍŒ™![]() £¨«Ûµ„M∫Õµ„Nµƒ◊¯±Í£ª
£¨«Ûµ„M∫Õµ„Nµƒ◊¯±Í£ª
£®3£©»Ù∏√∂˛¥Œ∫Ø ˝µƒÕºœÛø™ø⁄œÚœ¬£¨∂‘”⁄∏√∂˛¥Œ∫Ø ˝ÕºœÛ…œµƒ¡Ωµ„A£®x1£¨y1£©°¢B£®x2£¨y2£©£¨µ±x2°ð3 ±£¨æ˘”–y1°ðy2£¨«ÎΩ·∫œÕºœÛ£¨÷±Ω”–¥≥ˆx1µƒ»°÷µ∑∂Œß£Æ
°æ¥∞∏°ø£®1£©x£Ω1£ª£®2£©M£®5£¨![]() £©£¨N£®1£¨©Å4£©£ª£®3£©©Å1°Ðx1°Ð3
£©£¨N£®1£¨©Å4£©£ª£®3£©©Å1°Ðx1°Ð3
°æΩ‚Œˆ°ø
£®1£©Ω´∂˛¥Œ∫Ø ˝Ω‚Œˆ ΩªØŒ™y£Ωax2©Å2ax©Å2£Ωa£®x©Å1£©2©Åa©Å2£¨º¥ø…«Û∂‘≥∆÷·£ª
£®2£©”…“‚ø…÷™a£æ0£¨µ±©Å1°Ðx°Ð5 ±£¨x£Ω5 ±∫Ø ˝”–◊Ó¥Û÷µ£¨µ±x£Ω1 ±∫Ø ˝”–◊Ó–°÷µ£¨ø…»∑∂®M£®5£¨![]() £©£¨N£®1£¨©Å4£©£ª
£©£¨N£®1£¨©Å4£©£ª
£®3£©«Û≥ˆµ„£®3£¨0£©πÿ”⁄x£Ω1∂‘≥∆µƒµ„ «£®©Å1£¨0£©£¨”…“‚ø…÷™Aµƒ∫·◊¯±Í‘⁄©Å1£¨3÷ƺ‰ «¬˙◊„x2°ð3 ±£¨æ˘”–y1°ðy2£Æ
Ω‚£∫£®1£©y£Ωax2©Å2ax©Å2£Ωa£®x©Å1£©2©Åa©Å2£¨
°ý∂‘≥∆÷·Œ™x£Ω1£¨
π ¥∞∏Œ™x£Ω1£ª
£®2£©°þ∫Ø ˝µƒø™ø⁄œÚ…œ£¨
°ýa£æ0£¨
µ±©Å1°Ðx°Ð5 ±£¨x£Ω5 ±∫Ø ˝”–◊Ó¥Û÷µ£¨µ±x£Ω1 ±∫Ø ˝”–◊Ó–°÷µ£¨
°þ◊Ó∏þµ„Mµƒ◊ð◊¯±Í «![]() £¨
£¨
°ýµ±x£Ω5 ±y£Ω![]() £¨
£¨
°ýa£Ω2£¨
°ýM£®5£¨![]() £©£¨N£®1£¨©Å4£©£ª
£©£¨N£®1£¨©Å4£©£ª
£®3£©°þ∫Ø ˝µƒø™ø⁄œÚœ¬£¨
°ýa£º0£¨
£®3£¨0£©πÿ”⁄x£Ω1∂‘≥∆µƒµ„ «£®©Å1£¨0£©£¨
°þµ±x2°ð3 ±£¨æ˘”–y1°ðy2£¨
°ý©Å1°Ðx1°Ð3£Æ


 ÓºŸ◊˜“µ ÓºŸøÏ¿÷¡∑Œ˜∞≤≥ˆ∞Ê…Áœµ¡–¥∞∏
ÓºŸ◊˜“µ ÓºŸøÏ¿÷¡∑Œ˜∞≤≥ˆ∞Ê…Áœµ¡–¥∞∏ –¬ªÓ¡¶◊Ð∂Ø‘± Óœµ¡–¥∞∏
–¬ªÓ¡¶◊Ð∂Ø‘± Óœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœþ![]() æ≠π˝µ„
æ≠π˝µ„![]() ∫Õµ„
∫Õµ„![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() .
.
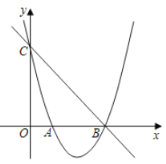
£®1£©«Û¥À≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©»Ùµ„![]() «÷±œþ
«÷±œþ![]() œ¬∑Ωµƒ≈◊ŒÔœþ…œ“ª∂ص„£®≤ªµ„
œ¬∑Ωµƒ≈◊ŒÔœþ…œ“ª∂ص„£®≤ªµ„![]() £¨
£¨![]() ÷ÿ∫œ£©£¨π˝µ„
÷ÿ∫œ£©£¨π˝µ„![]() ◊˜
◊˜![]() ÷·µƒ∆Ω––œþΩª÷±œþ
÷·µƒ∆Ω––œþΩª÷±œþ![]() ”⁄µ„
”⁄µ„![]() £¨…˵„
£¨…˵„![]() µƒ∫·◊¯±ÍŒ™
µƒ∫·◊¯±ÍŒ™![]() .
.
¢Ÿ”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æœþ∂Œ
µƒ¥˙ ˝ Ω±Ì æœþ∂Œ![]() µƒ≥§£ª
µƒ≥§£ª
¢⁄¡¨Ω”![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ√ʪ˝◊Ó¥Û ±µ„
µƒ√ʪ˝◊Ó¥Û ±µ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
£®3£©…Ë≈◊ŒÔœþµƒ∂‘≥∆÷·”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨µ„
£¨µ„![]() «≈◊ŒÔœþµƒ∂‘≥∆÷·…œ“ªµ„£¨
«≈◊ŒÔœþµƒ∂‘≥∆÷·…œ“ªµ„£¨![]() Œ™
Œ™![]() ÷·…œ“ªµ„£¨ «∑ҥʑ⁄’‚—˘µƒµ„
÷·…œ“ªµ„£¨ «∑ҥʑ⁄’‚—˘µƒµ„![]() ∫Õµ„
∫Õµ„![]() £¨ πµ√“‘µ„
£¨ πµ√“‘µ„![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() Œ™∂•µ„µƒÀƒ±þ–Œ «¡‚–Œ£ø»Áπ˚¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„
Œ™∂•µ„µƒÀƒ±þ–Œ «¡‚–Œ£ø»Áπ˚¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„![]() µƒ◊¯±Í£ª»Áπ˚≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
µƒ◊¯±Í£ª»Áπ˚≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øø™—ß≥ı£¨Œ“œÿƒ≥–£ø™’π°∞–¬—ß∆⁄°¢–¬’˜≥㨖¬∆¯œÛ°±»Î—ßœµ¡–ΩÔ˝ªÓ∂Ø£¨—µ¡∑¡ΩÃÏ∫Û£¨Œ™¡À‘⁄∫œ≥™÷–∏¯ƒ≥∞ý—ß…˙«°µ±µÿ∑÷≈‰…˘≤ø£¨∏√–£“Ù¿÷Ωà ¶¿Ó¿œ ¶Àʪ˙≥È»°—ß…˙ ‘≥™£¨∏˘æð ‘≥™«Èøˆ∞—À˘≥È—ß…˙∑÷≥…A°¢B°¢C°¢DÀƒ÷÷…˘≤øµ»º∂£¨≤¢∏˘æ𵻺∂Õ≥º∆Ω·π˚ªÊ÷∆¡À»ÁÕº1∫Õ»ÁÕº2¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£¨«Î∏˘æðÕº÷–Ã·π©µƒ–≈œ¢ÕÍ≥…“‘œ¬Œ £∫

£®1£©…»–ŒÕ≥º∆Õº÷–Dµ»∂‘”¶µƒ‘≤–ƒΩ«µƒ∂» ˝ «°° °°°„£¨≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®2£©“—÷™Aµ»…˘≤øµƒÕ¨—ß”–“ªŒª «ƒ–…˙£¨¿Ó¿œ ¶◊º±∏¥”’‚4ŒªÕ¨—ß÷–Àʪ˙—°‘Ò¡ΩŒªÕ¨—ßΩÃ∆‰À˚Õ¨—ߣ¨«Î”√¡–±Ì∑®ªÚª≠ ˜◊¥Õºµƒ∑Ω∑®«Û≥ˆ—°÷–µƒ¡Ω√˚Õ¨—ß«°∫√ «“ªƒ–“ª≈Ƶƒ∏≈¬ £ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
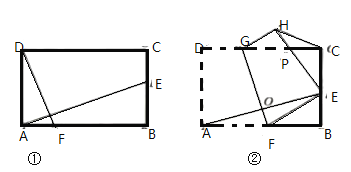
°æƒø°ø£®1£©»ÁÕº¢Ÿ£¨‘⁄æÿ–Œ![]() ÷–£¨
÷–£¨![]() ∑÷± «
∑÷± «![]() …œµƒµ„£¨«“
…œµƒµ„£¨«“![]() £¨«Û
£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©»ÁÕº¢⁄£¨‘⁄æÿ–Œ![]() ÷–
÷–![]() £®
£®![]() Œ™≥£ ˝£©£¨Ω´æÿ–Œ
Œ™≥£ ˝£©£¨Ω´æÿ–Œ![]() —ÿ
—ÿ![]() ’€µ˛£¨ πµ„
’€µ˛£¨ πµ„![]() ¬‰‘⁄
¬‰‘⁄![]() ±þ…œµƒµ„
±þ…œµƒµ„![]() ¥¶£¨µ√µΩÀƒ±þ–Œ
¥¶£¨µ√µΩÀƒ±þ–Œ![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨«Û
£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨¡¨Ω”![]() £¨µ±
£¨µ±![]() ±£¨»Ù
±£¨»Ù![]() £¨«Û
£¨«Û![]() µƒ≥§.
µƒ≥§.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝y£Ωax+bx+c£®a°Ÿ0£©µƒÕºœÛ»ÁÕºÀ˘ 棨“‘œ¬Ω·¬€÷–’˝»∑µƒ∏ˆ ˝ «£®°°°°£©
¢Ÿabc£æ0°¢¢⁄3a£æ2b°¢¢€m£®am+b£©°Ða©Åb£®mŒ™»Œ“‚ µ ˝£©°¢¢Ð4a©Å2b+c£º0£Æ
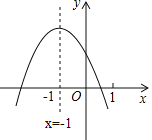
A.1B.2C.3D.4
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨µ„
£¨µ„![]() «
«![]() ÷ÿ–ƒ£¨¡¨Ω·
÷ÿ–ƒ£¨¡¨Ω·![]() ≤¢—”≥§Ωª
≤¢—”≥§Ωª![]() ”⁄µ„
”⁄µ„![]() £ª¡¨Ω·
£ª¡¨Ω·![]() ≤¢—”≥§Ωª
≤¢—”≥§Ωª![]() ”⁄µ„
”⁄µ„![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() .»Ù
.»Ù![]() µƒ√ʪ˝Œ™8£¨‘Ú
µƒ√ʪ˝Œ™8£¨‘Ú![]() µƒ√ʪ˝Œ™£® £©
µƒ√ʪ˝Œ™£® £©
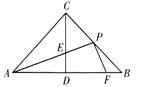
A.4B.2C.1D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ ![]() ”ÎX÷·Ωª”⁄µ„(®D3,0)£¨∆‰∂‘≥∆÷·Œ™÷±œþ
”ÎX÷·Ωª”⁄µ„(®D3,0)£¨∆‰∂‘≥∆÷·Œ™÷±œþ![]() ,Ω·∫œÕºœÛ∑÷Œˆœ¬¡–Ω·¬€:¢Ÿ
,Ω·∫œÕºœÛ∑÷Œˆœ¬¡–Ω·¬€:¢Ÿ![]() ; ¢⁄
; ¢⁄![]() £ª¢€µ±
£ª¢€µ±![]() ±£¨y ÀÊx µƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨¢Ð“ª‘™∂˛¥Œ∑Ω≥Ã
±£¨y ÀÊx µƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨¢Ð“ª‘™∂˛¥Œ∑Ω≥Ã![]() µƒ¡Ω∏˘∑÷±Œ™
µƒ¡Ω∏˘∑÷±Œ™![]() £ª¢ð»Ù
£ª¢ð»Ù![]() (
(![]() )Œ™∑Ω≥Ã
)Œ™∑Ω≥Ã![]() µƒ¡Ω∏ˆ∏˘£¨‘Ú
µƒ¡Ω∏ˆ∏˘£¨‘Ú![]() «“
«“![]() ,∆‰÷–’˝»∑µƒΩ·¬€”–( )
,∆‰÷–’˝»∑µƒΩ·¬€”–( )
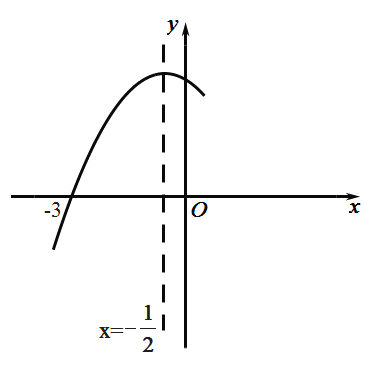
A.3∏ˆB.4∏ˆC.5∏ˆD.6∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø≈◊ŒÔœþy£Ωax2+bx+3æ≠π˝µ„A£®©Å1£¨0£©£¨B£®3£¨0£©£¨”Îy÷·Ωª”⁄µ„C£Æµ„D£®xD£¨yD£©Œ™≈◊ŒÔœþ…œ“ª∏ˆ∂ص„£¨∆‰÷–1£ºxD£º3£Æ¡¨Ω”AC£¨BC£¨DB£¨DC£Æ
£®1£©«Û∏√≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©µ±°˜BCDµƒ√ʪ˝µ»”⁄°˜AOCµƒ√ʪ˝µƒ2±∂ ±£¨«Ûµ„Dµƒ◊¯±Í£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨»Ùµ„M «x÷·…œ“ª∂ص„£¨µ„N «≈◊ŒÔœþ…œ“ª∂ص„£¨ ‘≈–∂œ «∑ҥʑ⁄’‚—˘µƒµ„M£¨ πµ√“‘µ„B£¨D£¨M£¨NŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£Æ»Ù¥Ê‘⁄£¨«Û≥ˆµ„Mµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
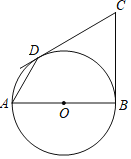
°æƒø°ø»ÁÕº£¨AB «°—O÷±æ∂£¨BC°ÕAB”⁄µ„B£¨µ„C «…‰œþBC…œ»Œ“‚“ªµ„£¨π˝µ„C◊˜CD«–°—O”⁄µ„D£¨¡¨Ω”AD£Æ
(1)«Û÷§£∫BC£ΩCD£ª
(2)»Ù°œC£Ω60°„£¨BC£Ω3£¨«ÛADµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com