
【题目】某地盛产樱桃,一年一度的樱桃节期间,很多果园推出了免费品尝和优惠采摘活动,其中甲、乙两家果园的樱桃品质相同,销售价格也相同,但推出了不同的采摘方案:
甲园 | 游客进园需购买 |
乙园 | 游客进园不需购买门票,采摘的樱桃在一定数量以内按原价购买,超过部分打折购买 |
小明和爸爸、妈妈在樱桃节期间也来采摘樱桃,若设他们的樱桃采摘量为![]() (千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为
(千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为![]() (元)在乙采摘园所需总费用为
(元)在乙采摘园所需总费用为![]() (元),图中的折线
(元),图中的折线![]() 表示
表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.

(1)①甲、乙两果园的樱桃单价为_____________元![]() 千克;
千克;
②直接写出![]() 的函数表达式:_________________,并在图中补画出
的函数表达式:_________________,并在图中补画出![]() 的函数图象;
的函数图象;
(2)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若小明一家当天所采摘的樱桃不少于![]() 千克,选择哪个采摘园更划算?请说明理由.
千克,选择哪个采摘园更划算?请说明理由.
【答案】(1)①![]() ;②
;②![]() ;
; ![]() 的函数图象详见解析;(2)
的函数图象详见解析;(2)![]() ;(3)当樱桃采摘量
;(3)当樱桃采摘量![]() 千克时,两家采摘园所需费用相同;当樱桃采摘量
千克时,两家采摘园所需费用相同;当樱桃采摘量![]() 的范围为
的范围为![]() 千克时,乙采摘园更划算.
千克时,乙采摘园更划算.
【解析】
(1)①根据单价=总价÷数量,即可求出甲、乙两采摘园优惠前的草莓销售价格;
②根据题意可求出y1与x的函数表达式,根据表达式利用两点法画出函数图象;
(2)结合图象利用待定系数法即可求出y2与x之间的函数关系式;
(3)分情形构建不等式即可解决问题.
解:(1)①![]()
②![]() ;
;
![]() 的函数图象如图所示:
的函数图象如图所示:
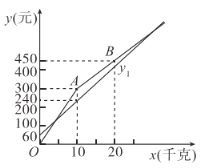
(2)由图可得,当![]() 时,
时,![]() ,
,
当![]() 时,设
时,设![]() .
.
将![]() 和
和![]() 代入
代入![]() ,
,
得![]() 解得
解得![]()
∴当![]() 时,
时,![]() .
.
![]()
(3)令![]() ,即
,即![]() ,解得
,解得![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() .
.
答:当樱桃采摘量![]() 千克时,两家采摘园所需费用相同;
千克时,两家采摘园所需费用相同;
当樱桃采摘量![]() 的范围为
的范围为![]() 千克时,乙采摘园更划算.
千克时,乙采摘园更划算.


科目:初中数学 来源: 题型:
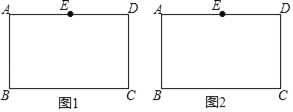
【题目】如图,在矩形ABCD中,点E为AD的中点,不用圆规、量角器等工具,只用无刻度的直尺作图.
(1)如图1,在BC上找点F,使点F是BC的中点;
(2)如图2,连接AC,在AC上取两点P,Q,使P,Q是AC的三等分点.
查看答案和解析>>
科目:初中数学 来源: 题型:
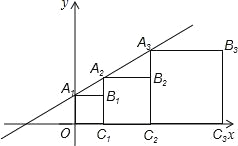
【题目】在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是 ,点Bn的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
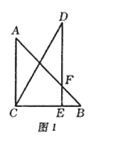
【题目】把一副三角板按如图1所示放置,其中点![]() 在
在![]() 边上,
边上,![]() ,斜边
,斜边![]() .将三角板
.将三角板![]() 绕点
绕点![]() 顺时针旋转,记旋转角为
顺时针旋转,记旋转角为![]() .
.
(1)在图1中,设![]() 与
与![]() 的交点为
的交点为![]() ,则线段AF的长为 ;
,则线段AF的长为 ;
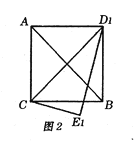
(2)当![]() 时,三角板
时,三角板![]() 旋转到
旋转到![]() ,的位置(如图2所示),连接
,的位置(如图2所示),连接![]() ,请判断四边形
,请判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
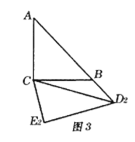
(3)当三角板![]() 旋转到
旋转到![]() 的位置(如图3所示)时,此时点
的位置(如图3所示)时,此时点![]() 恰好在
恰好在![]() 的延长线上.①求旋转角
的延长线上.①求旋转角![]() 的度数;②求线段
的度数;②求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
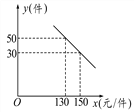
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为40cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于52cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于48cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com