（本小题满分10分）
观察思考
某种在同一平面进行传动的机械装置如图14-1，图14-2是它的示意图．其工作原理是：滑块Q在平直滑道l上可以左右滑动，在Q滑动的过程中，连杆PQ也随之运动，并且PQ带动连杆OP绕固定点O摆动．在摆动过程中，两连杆的接点P在以OP为半径的⊙O上运动．数学兴趣小组为进一步研究其中所蕴含的数学知识，过点O作OH ⊥l于点H，并测得OH = 4分米，PQ = 3分米，OP = 2分米．
解决问题
（1）点Q与点O间的最小距离是 分米；点Q与点O间的最大距离是 分米；点Q在l上滑到最左端的位置与滑到最右端位置间的距离是 分米．
（2）
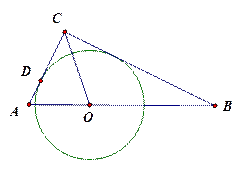
如图14-3，小明同学说：“当点Q滑动到点H的位置时，PQ与⊙O是相切的．”你认为他的判断对吗？为什么？
（3）①小丽同学发现：“当点P运动到OH上时，点P到l的距离最小．”事实上，还存在着点P到l距离最大的位置，此时，点P到l的距离是 分米；
②当OP绕点O左右摆动时，所扫过的区域为扇形，求这个扇形面积最大时圆心角的度数．
于点D，连结BD、BC，
，
，则BD= 
