【题目】如图，小明从路灯下A处向前走了5米，发现自己在地面上的影子长DE是2米，如果小明的身高为1.6米，那么路灯离地面的高度AB是（ ）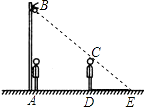 
A.4米
B.5.6米
C.2.2米
D.12.5米
【答案】B
【解析】解：由图知，DE=2米，CD=1.6米，AD=5米， ∴AE=AD+DE=5+2=7米
∵CD∥AB，
∴△ECD∽△EBA
∴ 
= 
，即 
= 
，
解得AB=5.6（米）．
故选B．
【考点精析】认真审题，首先需要了解相似三角形的应用(测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解)，还要掌握中心投影(手电筒、路灯和台灯的光线可以看成是从一个点发出的，这样的光线所形成的投影称为中心投影；作一物体中心投影的方法：过投影中心与物体顶端作直线，直线与投影面的交点与物体的底端之间的线段即为物体的影子)的相关知识才是答题的关键．
科目：初中数学 来源： 题型：
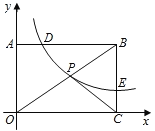
【题目】如图，已知矩形OABC中，OA＝3，AB＝4，双曲线y＝
（k＞0与矩形两边AB、BC分 别交于点D、E，且BD＝2AD﹒
（1）求此双曲线的函数表达式及点E的坐标；
（2）若矩形OABC的对角线OB与双曲线相交于点P，连结PC，求△POC的面积﹒
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A（1，6）和点B在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5．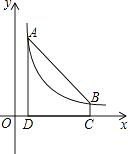 
（1）求反比例函数的表达式和点B的坐标；
（2）连接AB，在线段DC上是否存在一点E，使△ABE的面积等于5？若存在，求出点E的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC是等边三角形，以AC为直径的⊙O分别交AB，BC于点D，E，点F在AB的延长线上，2∠BCF=∠BAC．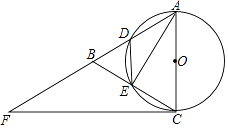 
（1）求∠ADE的度数．
（2）求证：直线CF是⊙O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在一块菱形菜地ABCD中，对角线AC与BD相交于点O，若在菱形菜地内均匀地撒上种子，则种子落在阴影部分的概率是（ ）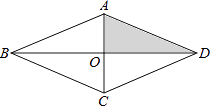 
A.1
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
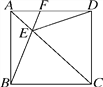
【题目】在正方形ABCD中，AC为对角线，点E为AC上一点，连接EB，ED.
(1)求证：△BEC≌△DEC；
(2)延长BE交AD于点F，当∠BED＝120°时，求∠EFD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，∠BAD=60°，点M是AB的中点，P是对角线AC上的一个动点，若PM+PB的最小值是9，则AB的长是（ ）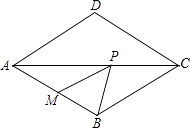 
A.6 
B.3
C.9
D.4.5
查看答案和解析>>
科目：初中数学 来源： 题型：
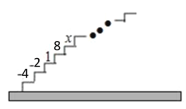
【题目】如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着﹣4，﹣2，1，8，且任意相邻四个台阶上数的和都相等．
尝试：（1）求前4个台阶上数的和是多少？
（2）求第5个台阶上的数x是多少？
应用： 求从下到上39个台阶上数的和．
发现：试用含k（k为正整数）的代数式表示出数“1”所在的台阶数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若一次函数y=kx+b的图象如图所示，则k，b的值可能为（ ）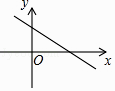
A.k=3，b=3
B.k=3，b=﹣3
C.k=﹣3，b=3
D.k=﹣3，b=﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com