
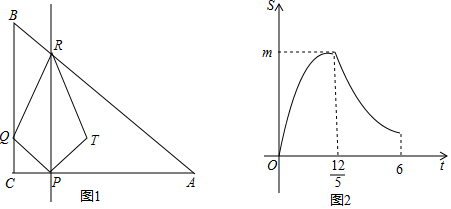
分析 (1)根据题意得:△CQP是等腰直角三角形,从图1中看,重叠部分的图形都是三角形,随着时间的增大先变大,再变小,与图2结合,发现最大时,即t=6时,Q与B重合,此时T、R都在斜边AB上,且CP=CQ=$\frac{12}{5}$,如图3,根据条件先求出AC和BC的长,由面积公式可以得出四边形RQPT的面积,根据对称可知,这个四边形面积是所求三角形面积的2倍,计算得出结论;
(2)根据(1)中求出的两直角边的长度,分两种情况:
①当0<t≤$\frac{12}{5}$时,如图4,重叠部分面积就是△PRT的面积,由平行相似先求PR的长,利用四边形面积公式可求出S关于t的函数关系式;
②当$\frac{12}{5}$<t≤6时,如图5,作高线ED,重叠部分面积是△PRE的面积,根据相似列比例式求DE的长,再代入面积公式进行计算.
解答 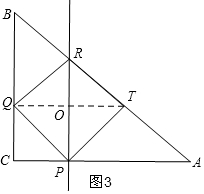 解:(1)由题意得:CP=CQ=t,
解:(1)由题意得:CP=CQ=t,
∵∠ACB=90°,
∴△CQP是等腰直角三角形,
由图2得:0<t≤6,即t=6时,Q与B重合,
∴BC=6,
从图2中得:t=$\frac{12}{5}$时,S最大,
即如图3所示,连接QT,此时T、R都在斜边AB上,且CP=CQ=$\frac{12}{5}$,
由折叠得:∠QRP=∠TRP,QR=RT,Q、T关于直线PR对称,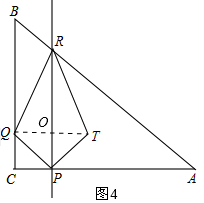
∴PR是线段QT的垂直平分线,
∴QT=2OQ=2CP=2×$\frac{12}{5}$=$\frac{24}{5}$,
∵PR⊥AC,BC⊥AC,
∴PR∥BC,
∴∠B=∠TRP,∠QRP=∠BQR,
∴∠B=∠BQR,
∴BR=QR,
∴BR=RT,
∴OR是△BQT的中位线,
∴OR=$\frac{1}{2}$BQ=$\frac{1}{2}$(6-$\frac{12}{5}$)=$\frac{9}{5}$,
∵QT∥AC,
∴△RQT∽△BCA,
∴$\frac{QT}{AC}=\frac{BQ}{BC}$,
∴$\frac{\frac{24}{5}}{AC}=\frac{\frac{18}{5}}{6}$,
∴AC=8,
∴S四边形QPTR=S△QRT+S△QPT=$\frac{1}{2}$QT•OR+$\frac{1}{2}$QT•OP=$\frac{1}{2}$QT•PR=$\frac{1}{2}$×$\frac{24}{5}$×$(\frac{12}{5}+\frac{9}{5})$=$\frac{252}{25}$,
∴S=S△PRT=$\frac{1}{2}$×$\frac{252}{25}$=$\frac{126}{25}$,
即m=$\frac{126}{25}$,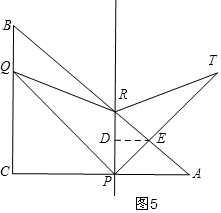
故答案为:等腰直角,$\frac{126}{25}$;
(2)分两种情况:
①当0<t≤$\frac{12}{5}$时,如图4,连接QT,交PR于O,
∵PR∥BC,
∴△APR∽△ACB,
∴$\frac{PR}{BC}=\frac{AP}{AC}$,
∴$\frac{PR}{6}=\frac{8-t}{8}$,
∴PR=$\frac{3(8-t)}{4}$,
∴S=S△PRQ=$\frac{1}{2}$S四边形RQPT=$\frac{1}{2}$×$\frac{1}{2}$×QT×PR=$\frac{1}{4}$×2t×$\frac{3}{4}(8-t)$=-$\frac{3}{8}{t}^{2}$+3t,
②当$\frac{12}{5}$<t≤6时,如图5,设PT与AB交点为E,过E作ED⊥PR于D,
由对称得:∠DPE=∠DEP=45°,
∵∠PDE=90°,
∴△PDE是等腰直角三角形,
∴PD=DE,
∵DE∥AC,
∴△RDE∽△RPA,
由(1)得△RPA∽△BCA,
∴△RDE∽△BCA,
∴$\frac{DR}{BC}=\frac{DE}{AC}$,
∴$\frac{DR}{6}=\frac{DE}{8}$,
∴DR=$\frac{3}{4}$DE=$\frac{3}{4}$PD,
同理得:PR=$\frac{3(8-t)}{4}$,
∴PR=DR+PD,
即$\frac{3(8-t)}{4}$=$\frac{3}{4}$PD+PD,
∴PD=DE=$\frac{3(8-t)}{7}$,
∴S=S△PRE=$\frac{1}{2}$PR•DE=$\frac{1}{2}$×$\frac{3(8-t)}{4}$×$\frac{3(8-t)}{7}$,
∴S=$\frac{9}{56}{t}^{2}$-$\frac{18}{7}$t+$\frac{72}{7}$,
综上所述,S关于t的函数关系式为:S=$\left\{\begin{array}{l}{-\frac{3}{8}{t}^{2}+3t(0<t≤\frac{12}{5})}\\{\frac{9}{56}{t}^{2}-\frac{18}{7}t+\frac{72}{7}(\frac{12}{5}<t≤6)}\end{array}\right.$.
点评 本题是动点问题的函数图象,考查了轴对称的性质、等腰直角三角形、相似三角形的性质和判定,综合性较强,本题的关键是能根据图2分别计算两直角边的长.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
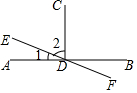 如图,直线AB、EF相交于点D,∠BDC=90°,∠ADC是∠BDC的补角.
如图,直线AB、EF相交于点D,∠BDC=90°,∠ADC是∠BDC的补角.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com